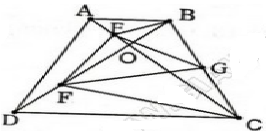
cho hình thang ABCD(AB song song với CD).kẻ hai đường chéo AC và BD cắt nhau tại O cho tam giác ABO đều.các điểm E,F,G lần lượt là trung điểm của các đoạn thẳng OA,OD và BC .Chứng minh tam giác EFG đều
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


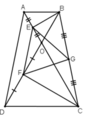

ΔAOB đều ⇒ BE là đường trung tuyến đồng thời là đường cao
⇒ BE ⊥ AO
⇒ ΔBEC vuông tại E
Mà EG là đường trung tuyến
⇒ 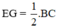 (1)
(1)
ΔCOD đều ⇒ CF là đường trung tuyến đồng thời là đường cao
⇒ CF ⊥ OD
⇒ ΔBFC vuông tại F
Mà FG là đường trung tuyến
⇒ 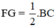 (2)
(2)
Hình thang ABCD (AB// CD) có: AC = AO + OC = OB + OD = BD
⇒ ABCD là hình thang cân
⇒ AD = BC.
ΔAOD có: AE = EO, FO = FD
⇒ EF là đường trung bình của ΔAOD
⇒ 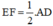
Mà AD = BC (cmt)
⇒ 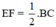 (3)
(3)
Từ (1); (2); (3) suy ra EF = FG = GE ⇒ ΔEFG đều (đpcm).

Vì OE = AE và OF = DF => EF là đường TB của tam giác OAD => EF = AD/2 (1)
Vì ABCD là hình thang => góc OAB = OCD = 60* và ODC = OBA = 60*
==> tam giác OCD đều
∆ OCD đều có CF là đường trung tuyến nên đồng thời là đường cao => CF _l_ BD
=> tam giác BCF vuông tại F có trung tuyến FG => FG = BC / 2 (2)
Tương tự ==> EG = BC / 2 (3)
Vì 2 tam giác OAB và OCD đều => OA = OB và OC = OD
=> OA + OC = OB + OD <=> AC = BD => ABCD là hình thang cân => AD = BC (4)
Từ (1)(2)(3)(4) => EF = EG = FG => tam giác EFG đều
mọi người giúp mình với!!! mình cảm ơn nhiều
cho hình thang cân ABCD có góc ACD=60 độ. O là giao điểm của 2 đường chéo. gọi E,F,G theo thứ tự là trung điểm của OA,OD,BC. tam giác EFG là tam giác gì? tại sao?


a) ABCD là hình thang nên AB//CD
CD=2AB ==>AB/CD=1/2
AB//CD, áp dụng định lý Ta-let, ta có
OA/OC=OB/OD=AB/CD=1/2
=>OA/OC=1/2 => OC=2OA
B) Ta có : OA/OC=OB/OD=AB/CD=1/2
==> OD/OB = 2 ==>OD = 2OB
*xét: OC/AC = 2OA/(OA + OC) = 2OA/(OA + 2OA) = 2OA/3OA = 2/3(1);
OD/BD = 2OB/(OD + OB) = 2OB/(2OB + OB) = 2/3(2)
*từ (1),(2) =>OC/AC = OD/BD = 2/3
=>O là trọng tâm tam giác FCD
c)
Vì một đường thẳng song song với AB và CD lần lượt cắt các đoạn thẳng AD, BD,AC và BC tại M, I,K và N nên KN//AB ,IM//AB và IN//AB
MI//AB, áp dụng hệ quả của định lý Ta-let, ta có
MI/AB = DM/AD = DI/IB (1)
IN//AB, áp dụng định lý Ta-let, ta có
CN/BC=DI/IB (2)
Từ (1) và (2), ta có
DM/AD=CN/BC
d)
KN//AB, áp dụng hệ quả của định lý Ta-let, ta có
KN/AB=CN/BC
Ta có :KN/AB=CN/BC và MI/AB=DM/AD
mà DM/AD=CN/BC nên KN/AB=MI/AB => KN=MI

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)

Bài 1:
Áp dụng định lý Talet cho $EO\parallel DC$:
$\frac{OE}{DC}=\frac{AO}{AC}(1)$
Áp dụng định lý Talet cho $OF\parallel DC$:
$\frac{OF}{DC}=\frac{OB}{BD}(2)$
Áp dụng định lý Talet cho $AB\parallel CD$:
$\frac{OA}{OC}=\frac{OB}{OD}\Leftrightarrow \frac{OA}{OA+OC}=\frac{OB}{OB+OD}\Leftrightarrow \frac{OA}{AC}=\frac{OB}{BD}(3)$
Từ $(1);(2);(3)\Rightarrow \frac{OE}{DC}=\frac{OF}{DC}$
$\Rightarrow OE=OF$ (đpcm)