cho ΔABC cân tại A có đường phân giác AD và đường trung tuyến BE cắt nhau tại H
a, Chứng minh ΔADB=ΔADC
b, Chứng minh ΔBHC là tam giác cân
c, Trên tia đối của tia EB lấy F sao cho EH=EF . Gọi G là giao điểm của FD với CH . Chứng minh BG đi qua trung điểm I của CF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 5 2016
Xét tam giác ABD và ACD có
AB=AC (tam giác ABC cân tại A)
Góc B = góc C ( 2 góc ở đáy của tam giác cân)
Canh AD chung
Suy ra tam giác ABD= tam giác ACD
Nen goc BAD=CAD(2 goc tuong ung)
Nên AD là tia phân giác của góc A
Suy ra AD là đường phân giác ,đường cao,đường trung trực,đường trung tuyến(tính chất tam giác cân)
17 tháng 9 2023
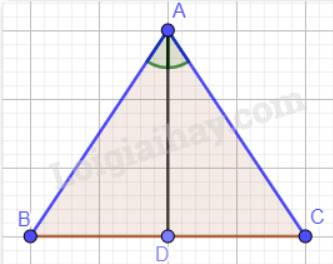
Xét hai tam giác ABD và ACD:
AB = AC (tam giác ABC cân tại A);
\(\widehat {BAD} = \widehat {CAD}\)(AD là phân giác của góc A);
AD chung.
Vậy \(\Delta ABD = \Delta ACD\)(c.g.c).
Suy ra: BD = CD ( 2 cạnh tương ứng) hay D là trung điểm của cạnh BC. Vậy AD là đường trung tuyến của tam giác ABC.
KV
17 tháng 9 2023
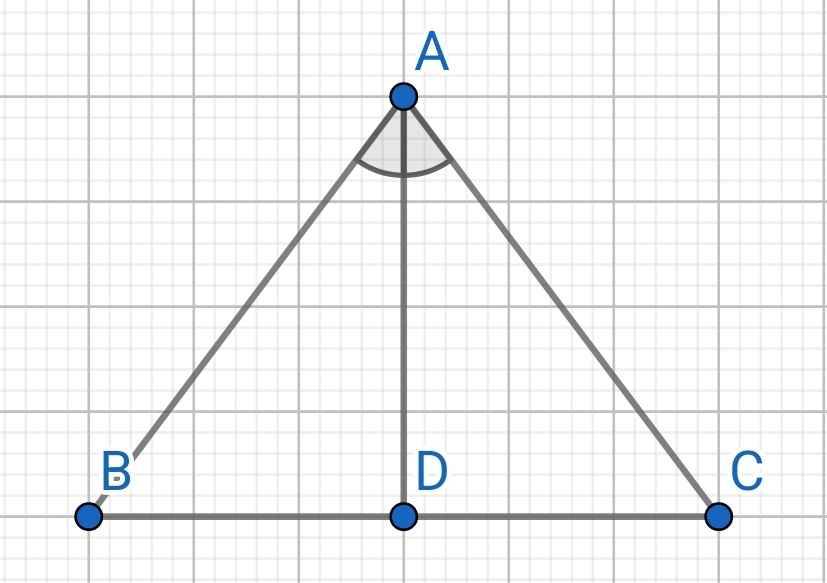Do ∆ABC cân tại A
⇒ AB = AC và ∠ABC = ∠ACB
⇒ ∠ABD = ∠ACD
Do AD là đường phân giác của ∠BAC
⇒ ∠BAD = ∠CAD
Xét ∆ABD và ∆ACD có:
∠BAD = ∠CAD (cmt)
AB = AC (cmt)
∠ABD = ∠ACD (cmt)
⇒ ∆ABD = ∆ACD (g-c-g)
⇒ BD = CD (hai cạnh tương ứng)
⇒ D là trung điểm của BC
Vậy AD là đường trung tuyến của ∆ABC
29 tháng 3 2018
ta có:\(AD\)là tia phân giác của góc \(\widehat{BAC}\)
Mà \(\Delta ABC\)cân tại A
\(\Rightarrow\)\(AD\)là trung tuyến của\(\widehat{BAC}\)(trong \(\Delta\)cânđường phân giác đòng thời à đường trung tuyến ứng vs cạch đáy)
có thể ghi gọn hơn chỉ giải thik cho hỉu thui
22 tháng 4 2018
a) So sánh AB và BC
b) Chứng minh CH đi qua trung điểm của cạnh AB
C) Chứng minh 3 điểm A, H, K thẳng hàng
KV
3 tháng 3 2023
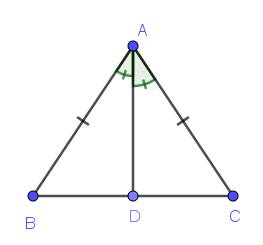
Xét \(\Delta ABD\) và \(\Delta ACD\) có:
AB = AC (gt)
AD là cạnh chung
\(\widehat{BAD}=\widehat{CAD}\) (do AD là tia phân giác)
\(\Rightarrow\Delta ABD=\Delta ACD\left(c-g-c\right)\)
\(\Rightarrow BD=CD\) (hai cạnh tương ứng)
\(\Rightarrow D\) là trung điểm của BC
\(\Rightarrow AD\) là đường trung tuyến của \(\Delta ABC\)
3 tháng 3 2023
Ta co: ΔABC cân tại A
mà AD là đường phân giác
nên AD là đường trung tuyến của ΔABC
24 tháng 6 2023
a: Xét ΔABH và ΔACH có
AB=AC
góc BAH=góc CAH
AH chung
=>ΔABH=ΔACH
=>BH=CH
b: Xét ΔEAH và ΔECF có
góc EAH=góc ECF
EA=EC
góc AEH=góc CEF
=>ΔEAH=ΔECF
=>EH=EF
a: Xét ΔADB và ΔADC có
AD chung
\(\widehat{BAD}=\widehat{CAD}\)
AB=AC
Do đó: ΔADB=ΔADC
b: ΔADB=ΔADC
=>DB=DC
=>D là trung điểm của BC
ΔABD=ΔACD
=>\(\widehat{ADB}=\widehat{ADC}\)
mà \(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
nên \(\widehat{ADB}=\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
=>AD\(\perp\)BC
Xét ΔHBC có
HD là đường trung tuyến
HD là đường cao
Do đó ΔHBC cân tại H
c: Xét ΔABC có
BE,AD là các đường trung tuyến
BE cắt AD tại H
Do đó: H là trọng tâm của ΔABC
=>BH=2HE
mà HF=2HE
nên BH=HF
=>H là trung điểm của BF
Xét ΔFBC có
FD,CH là các đường trung tuyến
FD cắt CH tại G
Do đó: G là trọng tâm của ΔFBC
=>BG đi qua trung điểm của CF