cho tam giác ABC vuông tại A có AD là đường phân giác. tính các cạnh của tam giac ABC biết AD=4, DC=5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(AB^2+AC^2=BC^2\Rightarrow BC^2=\left(\frac{3}{5}BC\right)^2+AC^2\)
\(\Leftrightarrow AC^2=\frac{16}{25}BC^2\Leftrightarrow AC=\frac{4}{5}BC\)
* Áp dụng hệ thức :
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{144}=\frac{1}{\frac{9}{25}BC^2}+\frac{1}{\frac{16}{25}BC^2}\)
\(\Leftrightarrow\frac{1}{144}=\frac{\frac{16}{25}BC^2+\frac{9}{25}BC^2}{\frac{16}{25}BC^2.\frac{9}{25}BC^2}\Rightarrow144BC^2=\frac{144}{625}BC^4\)
\(\Leftrightarrow\frac{144}{625}BC^2-144=0\Leftrightarrow BC^2=144.\frac{625}{144}=625\Leftrightarrow BC=25\)cm
\(\Rightarrow AB=\frac{3}{5}BC=\frac{3}{5}.25=\frac{75}{5}=15\)cm
\(\Rightarrow AC=\frac{4}{5}BC=\frac{4}{5}.25=\frac{100}{5}=20\)
Chu vi tam giác là : \(P_{ABC}=AB+BC+AB=15+20+25=60\)cm2
b, Vì AD là phân giác nên : \(\frac{AB}{AC}=\frac{BD}{DC}=\frac{15}{20}=\frac{3}{4}\Rightarrow AB=\frac{3}{4}AC\)
Lại có : \(BC=BD+DC=15+20=35\)cm
Áp dụng định lí Pytago cho tam giác ABC vuông tại A
\(BC^2=AC^2+AB^2=AC^2+\left(\frac{3}{4}AC\right)^2\)
\(\Rightarrow\frac{25}{16}AC^2=1225\Leftrightarrow AC^2=\frac{16.1225}{25}=784\Leftrightarrow AC=28\)cm
\(\Rightarrow AB=\frac{3}{4}.28=21\)cm
* Áp dụng hệ thức : \(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\Rightarrow\frac{1}{AH^2}=\frac{AC^2+AB^2}{AB^2AC^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{784+441}{345744}\Leftrightarrow1225AH^2=345744\Leftrightarrow AH^2=\frac{7056}{25}\Leftrightarrow AH=\frac{84}{5}\)cm
* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{441}{35}=\frac{63}{5}\)cm
\(\Rightarrow HD=BD-BH=15-\frac{63}{5}=\frac{12}{5}\)cm
Áp dụng định lí Pytago cho tam giác AHD vuông tại H
\(AD^2=AH^2+HD^2=\left(\frac{84}{5}\right)^2+\left(\frac{12}{5}\right)^2=288\Rightarrow AD=12\sqrt{2}\)cm

1:
BC=15+20=35cm
AD là phân gíac
=>AB/BD=AC/CD
=>AB/3=AC/4=k
=>AB=3k; AC=4k
AB^2+AC^2=BC^2
=>25k^2=35^2
=>k=7
=>AB=21cm; AC=28cm
AH=21*28/35=16,8cm
\(AD=\dfrac{2\cdot21\cdot28}{21+28}\cdot cos45=12\sqrt{2}\left(cm\right)\)
2:
BC=căn 12^2+16^2=20cm
HB=AB^2/BC=12^2/20=7,2cm
HC=20-7,2=12,8cm

a, \(vì\)AD là phân giác suy ra góc BAD =góc DAC =45 ĐỘ
cos45 độ = AD/AB =4 /AB =1/ căn 2 suy ra AB =4 NHÂN CĂN 2
TH TỰ dùng sin 45 độ =dc/ac =5/ad =1/căn 2 suy ra AC =5 CĂN 2 ÁP DỤNG PITA GO TÌM RA CẠNH bc
b,

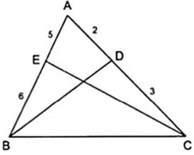
Áp dụng tính chất của các đường phân giác BD và CE của tam giác ABC ta được:
+ AB/BC = AD/DC = 2/3 = 4/6
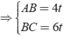 với t > 0
với t > 0
+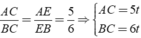
Theo giả thiết ta có: P A B C = A B + A C + B C = 15 t = 45 ⇒ t = 3
Vậy AB = 12( cm ); BC = 18( cm ); AC = 15( cm )

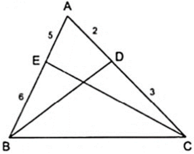
Áp dụng tính chất của các đường phân giác BD và CE của tam giác ABC ta được:
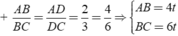 với t > 0
với t > 0
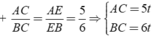
Theo giả thiết ta có: PABC = AB + AC + BC = 15t = 45 ⇒ t = 3
Vậy AB = 12( cm ); BC = 18( cm ); AC = 15( cm )

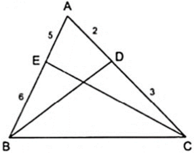
Áp dụng tính chất của các đường phân giác BD và CE của tam giác ABC ta được:
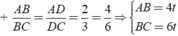 với t > 0
với t > 0
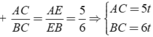
Theo giả thiết ta có: PABC = AB + AC + BC = 15t = 45 ⇒ t = 3
Vậy AB = 12( cm ); BC = 18( cm ); AC = 15( cm )

Bn có thể Kham Khảo ở chỗ này rất hiệu quả nè :
http://lazi.vn/edu/exercise/cho-tam-giac-abc-vuong-tai-a-co-ab-3cm-ac-4cm-duong-phan-giac-ad-duong-vuong-goc-voi-dc-cat-ac-o-e
nếu đúng thì cho mk nha


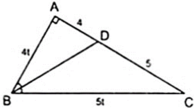
Áp dụng tính chất đường phân giác BD của tam giác
ABC, ta có:
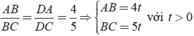 với t > 0
với t > 0
Áp dụng định lý Py – ta – go ta có:
B C 2 = A C 2 + A B 2 hay ( 5 t ) 2 = 9 2 + ( 4 t ) 2 ⇔ ( 3 t ) 2 = 9 2 ⇒ t = 3 (vì t > 0 )
Khi đó: AB = 12cm, BC = 15cm

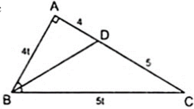
Áp dụng tính chất đường phân giác BD của tam giác ABC, ta có:
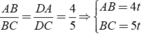 với t > 0
với t > 0
Áp dụng định lý Py – ta – go ta có:

Khi đó: AB = 12cm, BC = 15cm
Từ D hạ các đường vuông góc DH xống AC và DK xuống AB.
Tứ giác HDKA là hình vuông vì vậy \(AH^2+HD^2=AD^2\) suy ra \(2AH^2=4^2\Leftrightarrow AH=8\)\(\Leftrightarrow AH=2\sqrt{2}\left(cm\right)\).
Suy ra \(AH=HD=DK=AK=2\sqrt{2}\left(cm\right)\).
Áp dụng định lý Pi-ta-go trong tam HCD ta có: \(HC=\sqrt{DC^2-HD^2}=\sqrt{5^2-\left(2\sqrt{2}\right)^2}=\sqrt{17}\left(cm\right)\).
Suy ra \(AC=AH+HC=2\sqrt{2}+\sqrt{17}\left(cm\right)\).
Tam giác BDI đồng dạng với tam giác BCA nên: \(\frac{BD}{BC}=\frac{BI}{BA}=\frac{DI}{CA}\).
Suy ra \(\frac{BD}{BC}=\frac{DI}{CA}\Leftrightarrow\frac{BD}{BD+5}=\frac{2\sqrt{2}}{2\sqrt{2}+\sqrt{17}}\)\(BD=\frac{10\sqrt{2}}{\sqrt{17}}=\frac{10\sqrt{34}}{17}\left(cm\right)\).
\(BC=BD+DC=\frac{10\sqrt{34}}{17}+5\) (cm).
\(BI^2=BD^2-DI^2=\left(\frac{10\sqrt{34}}{17}\right)^2-\left(2\sqrt{2}\right)^2=\frac{64}{17}\).
Suy ra \(BI=\frac{8\sqrt{17}}{17}\left(cm\right)\).
\(AB=BI+IA=\frac{8\sqrt{17}}{17}+2\sqrt{2}\left(cm\right)\).