Tính tan (a+b) . Biết cosa = 3/5 và 0<a< pi/2 . Cosb = 12/13 và 3pi/2 < b< 2pi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\begin{array}{l}\cos \left( { - 30^\circ } \right) = \frac{{\sqrt 3 }}{2} > 0\\\sin \left( { - 30^\circ } \right) = - \frac{1}{2} < 0\\\tan \left( { - 30^\circ } \right) = - \frac{{\sqrt 3 }}{3} < 0\\\cot \left( { - 30^\circ } \right) = - \sqrt 3 < 0\end{array}\)

Do \(\frac{\pi }{2} < \frac{{5\pi }}{6} < \pi \) nên
\(\begin{array}{l}\cos \left( {\frac{{5\pi }}{6}} \right) < 0\\\sin \left( {\frac{{5\pi }}{6}} \right) > 0\\\tan \left( {\frac{{5\pi }}{6}} \right) < 0\\\cot \left( {\frac{{5\pi }}{6}} \right) < 0\end{array}\)

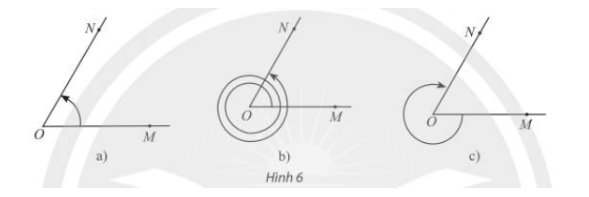
a, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(60^o\)
b, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(60^o+2\cdot360^o=780^o\)
c, Số đo của góc lượng giác (OM, ON) trong Hình 6 là \(\dfrac{5}{6}\cdot\left(-360^o\right)=-300^o\)
Công thức tổng quát của số đo góc lượng giác (OM, ON) \(=60^o+360^o\cdot k,k\in Z\)

Chọn B.
Dựa theo định nghĩa các giá trị lượng giác trên đường tròn lượng giác.
Khi M nằm trong góc phần tư thứ nhất thì sin α và cosα cùng dương hoặc khi M nằm trong góc phần tư thứ ba thì sinα và cosα cùng âm.

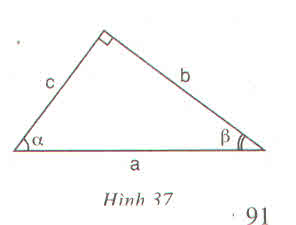
Xét ΔABC vuông tại A có
\(sinB=\dfrac{AC}{BC}\)
\(cosB=\dfrac{AB}{BC}\)
\(tanB=\dfrac{AC}{AB}\)
\(cotB=\dfrac{AB}{AC}\)
Xét ΔABC vuông tại A có
\(sinC=\dfrac{AB}{BC}\)
\(cosC=\dfrac{AC}{BC}\)
\(tanC=\dfrac{AB}{AC}\)
\(cotC=\dfrac{AC}{AB}\)
Nhận xét:
\(sinB=cosC\)
\(sinC=cosB\)
\(tanB=cotC\)
\(cotB=tanC\)

\(\begin{array}{l}\cos \left( {\alpha + \alpha } \right) = \cos 2\alpha = \cos \alpha \cos \alpha - \sin \alpha sin\alpha = {\cos ^2}\alpha - {\sin ^2}\alpha \\ = {\cos ^2}\alpha + {\sin ^2}\alpha - 2{\sin ^2}\alpha = 1 - 2{\sin ^2}\alpha = 2{\cos ^2}a - 1\end{array}\)
\(\tan 2\alpha = \tan \left( {\alpha + \alpha } \right) = \frac{{\tan \alpha + \tan \alpha }}{{1 - \tan \alpha .\tan \alpha }} = \frac{{2\tan a}}{{1 - {{\tan }^2}a}}\)
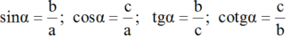

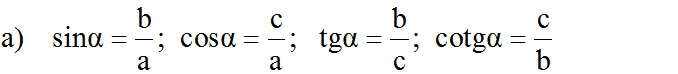
\(0< a< \dfrac{\Omega}{2}\)
=>\(sina>0\)
=>\(sina=\sqrt{1-cos^2a}=\dfrac{4}{5}\)
\(\dfrac{3}{2}\Omega< b< 2\Omega\)
=>\(sinb< 0\)
=>\(sinb=-\sqrt{1-\left(\dfrac{12}{13}\right)^2}=-\dfrac{5}{13}\)
\(tana=\dfrac{sina}{cosa}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)
\(tanb=\dfrac{sinb}{cosb}=\dfrac{-5}{13}:\dfrac{12}{13}=-\dfrac{5}{12}\)
\(tan\left(a+b\right)=\dfrac{tana+tanb}{1-tana\cdot tanb}\)
\(=\dfrac{\dfrac{4}{3}+\dfrac{-5}{12}}{1-\dfrac{4}{3}\cdot\dfrac{-5}{12}}=\dfrac{11}{12}:\left(1+\dfrac{20}{36}\right)=\dfrac{11}{12}:\dfrac{14}{9}\)
\(=\dfrac{11}{12}\cdot\dfrac{9}{14}=\dfrac{11\cdot3}{4\cdot14}=\dfrac{33}{56}\)
Giúp em vs ạ