78 + 32 - {90 - 1^100+(5^2 + 15)}
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
G
2 tháng 1 2022
Tham Khảo
ở vùng núi, khí hậu và thực vật thay đổi theo độ cao. Càng lên cao không khí càng loãng dần, cứ lên cao l00 m nhiệt độ không khí lại giảm 0,6°C. Từ trên độ cao khoảng 3000m ở đới ôn hoà và khoảng 5500 m ở đới nóng là nơi có băng tuyết phủ vĩnh viễn.
Sự thay đổi nhiệt độ, độ ẩm không khí từ chân núi lên đỉnh núi đã tạo nên sự phân tầng thực vật theo độ cao, gần giống như khi chúng ta đi từ vùng vĩ độ thấp lên vùng vĩ độ cao.
Khí hậu và thực vật còn thay đổi theo hướng của sườn núi. Những sườn núi lớn gió ẩm thường có mưa nhiều, cây cối tốt tươi hơn so với sườn khuất gió hoặc đón gió lạnh. Ở đới ôn hoà, trên những sườn núi đón ánh nắng, cây cối phát triển lên đến những độ cao lớn hơn phía sườn khuất nắng.
Trên các sườn núi có độ dốc lớn dễ xảy ra lũ quét, lở đất… khi mưa to kéo dài, đe doạ cuộc sống của người dân sống ờ các thung lũng phía dưới. Độ dốc lớn còn gây trở ngại cho việc đi lại và khai thác tài nguyên ở vùng núi.
27 tháng 12 2021
Các kiểu dữ liệu cơ bản: kiểu số nguyên, kiểu số thực, kiểu chuổi, kiểu kí tự
CM
2 tháng 11 2017
a) Cách giải các phương trình lượng giác cơ bản:
+ Phương trình sin x = a.
Nếu |a| > 1 ⇒ phương trình vô nghiệm.
Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho sin α = a.
Khi đó phương trình trở thành sin x = sin α
⇒ Phương trình có nghiệm: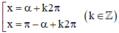 
+ Phương trình cos x = a.
Nếu |a| > 1 ⇒ phương trình vô nghiệm.
Nếu |a| ≤ 1 ⇒ tìm một cung α sao cho cos α = a.
Khi đó phương trình trở thành cos x = cos α.
⇒ Phương trình có nghiệm: x = ±α + k2π (k ∈ Z).
+ Phương trình tan x = a.
Tìm một cung α sao cho tan α = a.
Khi đó phương trình trở thành tan x = tan α.
⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).
+ Phương trình cot x = a
Tìm một cung α sao cho cot α = a.
Khi đó phương trình trở thành cot x = cot α.
⇒ Phương trình có nghiệm x = α + kπ (k ∈ Z).
b) Cách giải phương trình a.sin x + b.cos x = c.
+ Nếu a = 0 hoặc b = 0 ⇒ Phương trình lượng giác cơ bản .
+ a ≠ 0 và b ≠ 0. Chia cả hai vế của phương trình cho 
ta được:
Ta giải phương trình trên như phương trình lượng giác cơ bản.
VT
13 tháng 7 2018
Kể tên các loại máy cơ đơn giản: mặt phẳng nghiêng, đòn bẩy, ròng rọc (các em tự nêu ví dụ).
23 tháng 12 2016
Mặt phẳng nghiêng: Tấm ván nghiêng dung để đẩy hàng lên xe oto chẳng hạn
Ròng rọc: Cần kéo nước để kéo nước từ dưới lên
Đòn bẩy: búa nhổ đinh
\(78+32-\left\{90-1^{100}+\left(5^2+15\right)\right\}\)
\(=110-90+1^{100}-\left(25+15\right)\)
=20+1-40
=21-40=-19
tk
-19