Tính A = (1 - 1/22)(1 - 1/32)(1 - 1/42)...(1 - 1/n2) với điều kiện n thuộc N và n > 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 2 2021
a) uses crt;
var n,x,i:longint;
lt:real;
begin
clrscr;
write('Nhap co so n=');readln(n);
write('Nhap so mu x='); readln(x);
lt:=1;
for i:=1 to x do
lt:=lt*n;
writeln(n,'^',x,'=',lt:0:0);
readln;
end.
13 tháng 11 2023
\(B=1\cdot2\cdot3+2\cdot3\cdot4+...+\left(n-1\right)\cdot n\cdot\left(n+1\right)\)
=>\(4B=1\cdot2\cdot3\cdot4+2\cdot3\cdot4\cdot4+...+\left(n-1\right)\cdot n\left(n+1\right)\cdot4\)
=>\(4B=1\cdot2\cdot3\cdot4+2\cdot3\cdot4\left(5-1\right)+...+\left(n-1\right)\cdot n\left(n+1\right)\left[\left(n+2\right)-\left(n-2\right)\right]\)
=>\(4B=1\cdot2\cdot3\cdot4-1\cdot2\cdot3\cdot4+...+\left(n-2\right)\left(n-1\right)\cdot n\cdot\left(n+1\right)-\left(n-2\right)\cdot\left(n-1\right)\cdot n\cdot\left(n+1\right)+\left(n-1\right)\cdot n\left(n+1\right)\left(n+2\right)\)
=>\(4B=\left(n-1\right)\cdot n\cdot\left(n+1\right)\left(n+2\right)\)
=>\(B=\dfrac{\left(n-1\right)\cdot n\left(n+1\right)\left(n+2\right)}{4}\)
\(C=1\cdot4+2\cdot5+3\cdot6+...+n\left(n+3\right)\)
\(=1\cdot\left(1+3\right)+2\left(2+3\right)+...+n\left(n+3\right)\)
\(=\left(1^2+2^2+...+n^2\right)+3\left(1+2+...+n\right)\)
\(=\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}+3\cdot\dfrac{n\left(n+1\right)}{2}\)
\(=\dfrac{n\left(n+1\right)\left(2n+1\right)}{6}+\dfrac{3n\left(n+1\right)}{2}\)
\(=\dfrac{n\left(n+1\right)}{2}\cdot\left(\dfrac{2n+1}{3}+3\right)\)
\(=\dfrac{n\left(n+1\right)}{2}\cdot\dfrac{2n+1+9}{3}\)
\(=\dfrac{n\left(n+1\right)\left(n+5\right)}{3}\)
\(D=1^2+2^2+...+n^2\)
\(=1+\left(1+1\right)\cdot2+\left(1+2\right)\cdot3+...+\left(1+n-1\right)\cdot n\)
\(=1+2+3+...+n+\left(1\cdot2+2\cdot3+...+\left(n-1\right)\cdot n\right)\)
Đặt \(A=1+2+3+...+n;E=1\cdot2+2\cdot3+...+\left(n-1\right)\cdot n\)
\(E=1\cdot2+2\cdot3+...+\left(n-1\right)\cdot n\)
=>\(3E=1\cdot2\cdot3+2\cdot3\cdot3+...+\left(n-1\right)\cdot n\cdot3\)
=>\(3E=1\cdot2\cdot3+2\cdot3\cdot\left(4-1\right)+...+\left(n-1\right)\cdot n\left[\left(n+1\right)-\left(n-2\right)\right]\)
=>\(3E=1\cdot2\cdot3-1\cdot2\cdot3+2\cdot3\cdot4+...+\left(n-1\right)\cdot n\left(n-2\right)-\left(n-1\right)\cdot n\left(n-2\right)+\left(n-1\right)\cdot n\cdot\left(n+1\right)\)
=>\(3E=\left(n-1\right)\cdot n\left(n+1\right)=n^3-n\)
=>\(E=\dfrac{n^3-n}{3}\)
\(A=1+2+3+...+n\)
Số số hạng là n-1+1=n(số)
Tổng của dãy số là: \(A=\dfrac{n\left(n+1\right)}{2}\)
=>\(D=\dfrac{n^3-n}{3}+\dfrac{n\left(n+1\right)}{2}\)
\(=\dfrac{2n^3-2n+3n^2+3n}{6}\)
=>\(D=\dfrac{2n^3+3n^2+n}{6}\)
LE
0
E
21 tháng 1 2022
Với A1 = 12. Ta sẽ chứng minh An =1 + 3 + ... + (2n-1) = n2 (đáp án d)
Giả sử An đúng với n = k tức Ak = 1 + 3 + ... + (2k - 1) = k2. Ta sẽ chứng minh nó cũng đúng với Ak+1
Thật vậy: Ak+1 = 1 + 3 + ... + (2k-1) + (2k+1) = Ak + 2k + 1 = k2 + 2k + 1 = (k+1)2
Vậy...
AM
9 tháng 2 2022
Không biết đề có vấn đề không nữa, tại vì không có cách nào để rút được c ra hết do f(n+1)-f(n) kiểu gì c cũng bị khử. Tuy nhiên nếu xét trường hợp với mọi c thì thay n=3 trở lên giải ngược lại không có nghiệm c nào thỏa mãn hết hehe nên là mình nghĩ đề sẽ kiểu "với n=1 hoặc n=2" . Theo mình nghĩ là vậy...
Giả sử n=1 ta có:
\(f\left(1+1\right)-f\left(1\right)=1\Leftrightarrow f\left(2\right)-f\left(1\right)=1\Leftrightarrow4a+2b+c-a-b-c=1\Leftrightarrow3a+b=1\) (1)
Giả sử n=2 ta có:
\(f\left(2+1\right)-f\left(2\right)=4\Leftrightarrow f\left(3\right)-f\left(2\right)=4\Leftrightarrow9a+3b+c-4a-2b-c=4\Leftrightarrow5a+b=4\) (2)
Từ (1) và (2) ta có: \(\left\{{}\begin{matrix}3a+b=1\\5a+b=4\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a=\dfrac{3}{2}\\b=-\dfrac{7}{2}\end{matrix}\right.\)
\(\Rightarrow f\left(x\right)=\dfrac{3}{2}x^2-\dfrac{7}{2}x+c\) (với c là hằng số bất kì)
1 tháng 11 2023
a:
Số số hạng trong dãy M là:
(1002-12):10+1=100(số)
=>Sẽ có 50 cặp (1002;992); (982;972);....;(22;12) có hiệu bằng 10
\(M=1002-992+982-972+...+22-12\)
\(=\left(1002-992\right)+\left(982-972\right)+...+\left(22-12\right)\)
\(=10+10+...+10\)
=10*50=500
b: \(N=\left(202+182+...+42+22\right)-\left(192+172+...+32+12\right)\)
\(=\left(202-192\right)+\left(182-172\right)+...+\left(22-12\right)\)
=10+10+...+10
=10*10=100
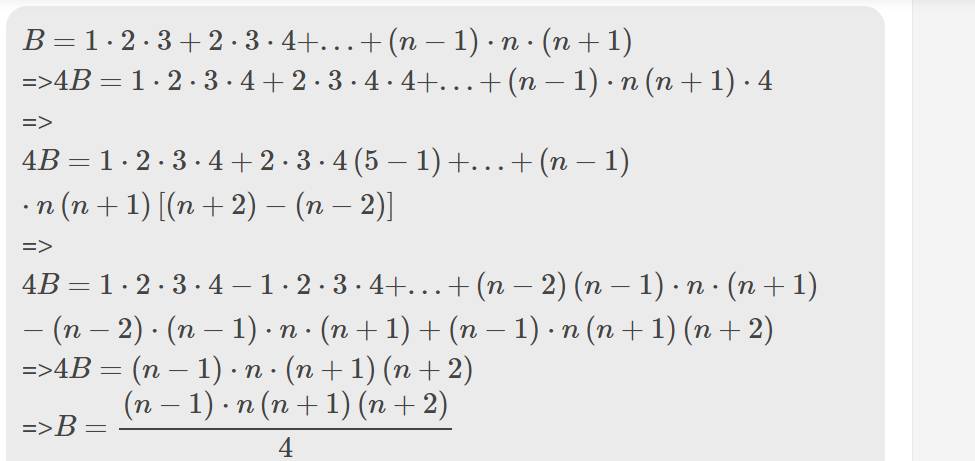
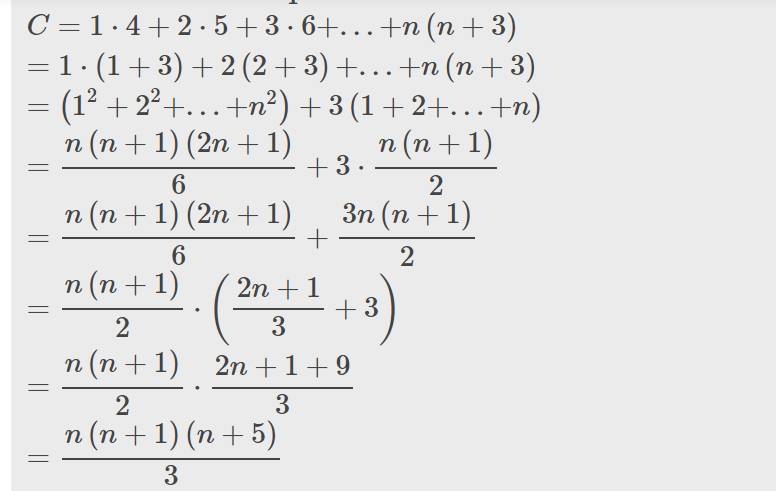
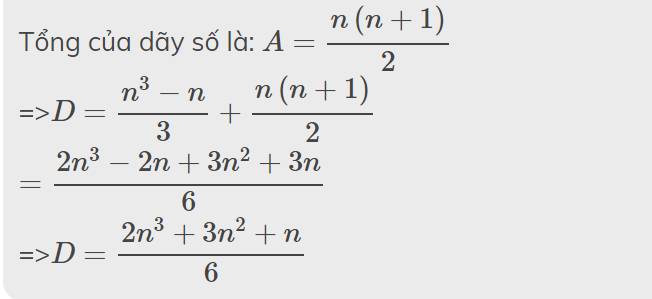
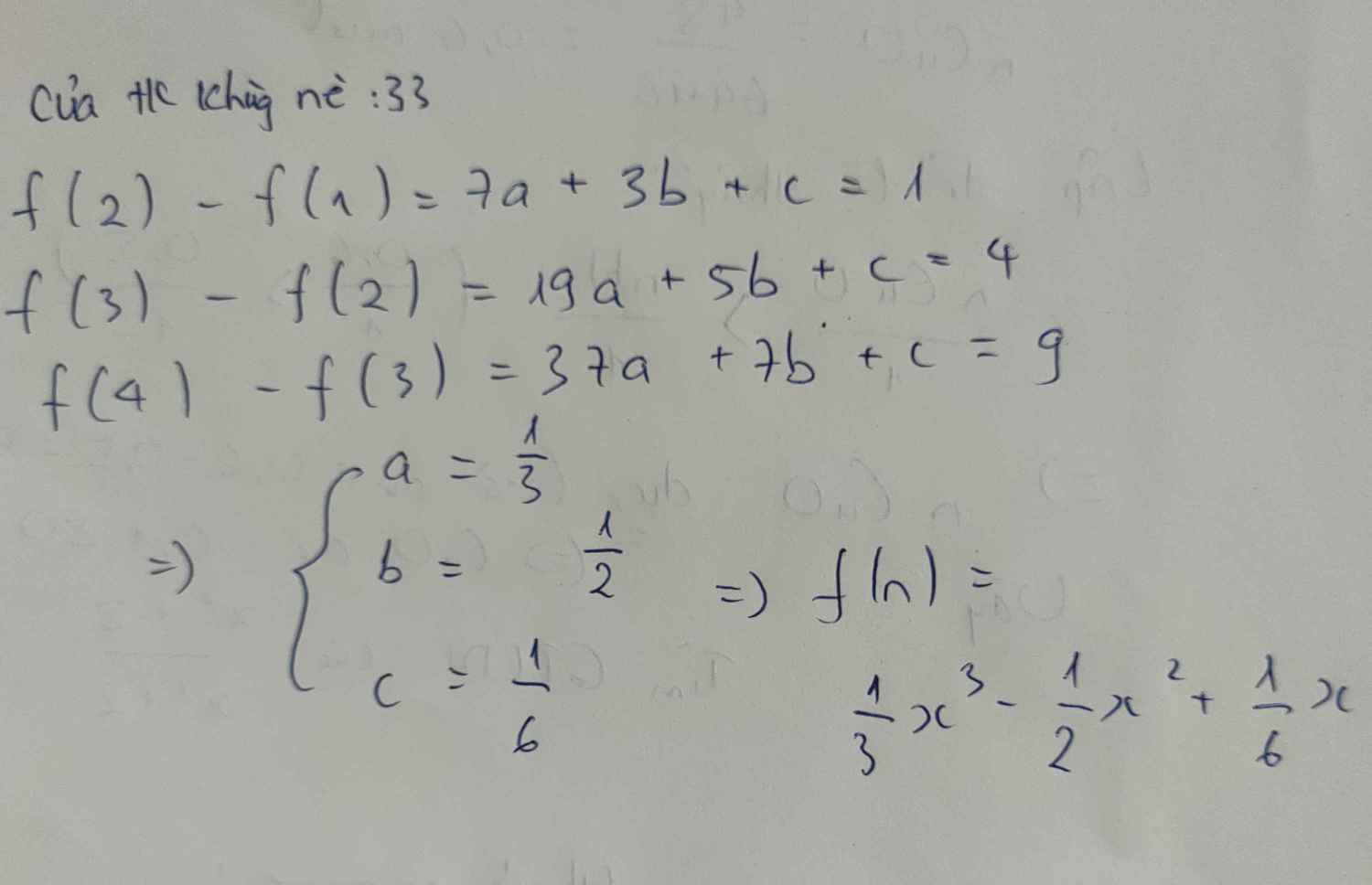
i wtan youm att jjjfdef the fifture haixx