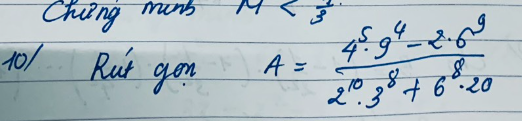
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
1) \(B=1:\dfrac{\left(x+2\right)\left(\sqrt{x}+1\right)+\left(x-1\right)\left(\sqrt{x}+1\right)-\left(\sqrt{x}+1\right)\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\left(x+\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)\left(x+\sqrt{x}+1\right)}{x\sqrt{x}-\sqrt{x}}=\dfrac{\left(x-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(x-1\right)}=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\)
2) \(VT=\dfrac{\left(6a+1\right)\left(a+6\right)+\left(6a-1\right)\left(a-6\right)}{a\left(a-6\right)\left(a+6\right)}.\dfrac{\left(a-6\right)\left(a+6\right)}{a^2+1}\)
\(=\dfrac{12a^2+12}{a\left(a^2+1\right)}=\dfrac{12\left(a^2+1\right)}{a\left(a^2+1\right)}=\dfrac{12}{a}=VP\)

a) \(B=\dfrac{x-\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{9-\sqrt{9}+1}{\sqrt{9}-1}=\dfrac{9-3+1}{3-1}=\dfrac{7}{2}\)
b) \(A=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)+2\left(\sqrt{x}-2\right)-9\sqrt{x}+3}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{x-3\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}=\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}+3}\)
c) \(A=\dfrac{\sqrt{x}-1}{\sqrt{x}+3}>0\Leftrightarrow\sqrt{x}-1>0\left(do.\sqrt{x}+3>0\right)\)
\(\Leftrightarrow\sqrt{x}>1\Leftrightarrow x>1\)
\(B=\dfrac{x-\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)+1}{\sqrt{x}-1}=\sqrt{x}+\dfrac{1}{\sqrt{x}-1}\)
Do \(\sqrt{x}>1\Leftrightarrow\sqrt{x}-1>0\)
Áp dụng BĐT Cauchy cho 2 số k âm:
\(B=\sqrt{x}-1+\dfrac{1}{\sqrt{x}-1}+1\ge2\sqrt{\left(\sqrt{x}-1\right).\dfrac{1}{\sqrt{x}-1}}+1=2+1=3\)
Dấu "=" xảy ra \(\Leftrightarrow\left(\sqrt{x}-1\right)^2=1\Leftrightarrow x=4\)

a) \(P=\left(\frac{\sqrt{x}}{\sqrt{x}-2}+\frac{1}{\sqrt{x}+2}-\frac{2}{4-x}\right):\frac{\sqrt{x}+3}{\sqrt{x}-2}\left(ĐK:x\ge0;x\ne4\right)\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+2\right)+\sqrt{x}-2+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\frac{\sqrt{x}-2}{\sqrt{x}+3}\)
\(=\frac{x+2\sqrt{x}+\sqrt{x}}{\sqrt{x}+2}\cdot\frac{1}{\sqrt{x}+3}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+3\right)}{\sqrt{x}+2}\cdot\frac{1}{\sqrt{x}+3}=\frac{\sqrt{x}}{\sqrt{x}+2}\)
b) Vì: \(\sqrt{x}+4>0,\forall x\inĐK\)
=> \(2\sqrt{x}+4>\sqrt{x}\)
=> \(\frac{\sqrt{x}}{2\sqrt{x}+4}< 0\)
=> \(\frac{\sqrt{x}}{\sqrt{x}+2}< 2\)
=>đpcm

`1)(a^[1/4]-b^[1/4])(a^[1/4]+b^[1/4])(a^[1/2]+b^[1/2])`
`=[(a^[1/4])^2-(b^[1/4])^2](a^[1/2]+b^[1/2])`
`=(a^[1/2]-b^[1/2])(a^[1/2]+b^[1/2])`
`=a-b`
`2)(a^[1/3]-b^[2/3])(a^[2/3]+a^[1/3]b^[2/3]+b^[4/3])`
`=(a^[1/3]-b^[2/3])[(a^[1/3])^2+a^[1/3]b^[2/3]+(b^[2/3])^2]`
`=(a^[1/3])^3-(b^[2/3])^3`
`=a-b^2`

a, \(\sqrt{\left(\sqrt{5}-4\right)^2}-\sqrt{5}+\sqrt{20}=4\)
\(VT=\sqrt{\left(4-\sqrt{5}\right)^2}-\sqrt{5}+\sqrt{20}=\left|4-\sqrt{5}\right|-\sqrt{5}+\sqrt{20}\)
\(=4-\sqrt{5}-\sqrt{5}+2\sqrt{5}=4\) hay \(VT=VP\)
Vậy ta có đpcm
b, Với \(x>0,x\ne4\)
\(P=\left(\frac{1}{\sqrt{x}+2}+\frac{1}{\sqrt{x}-2}\right):\frac{2}{x-2\sqrt{x}}\)
\(=\left(\frac{\sqrt{x}-2+\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\right):\frac{2}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\frac{2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}.\frac{\sqrt{x}\left(\sqrt{x}-2\right)}{2}=\frac{x}{\sqrt{x}+2}\)
1.
Giả sử điều trên là đúng ta có:
\( \left | \sqrt{5}-4 \right |-\sqrt{5}+\sqrt{20}=4\)
Ta có: \(4>\sqrt{5}\)
\(\Rightarrow 4-\sqrt{5}- \sqrt{5}+\sqrt{20}=4\)
\(\Leftrightarrow 4-\sqrt{20}+\sqrt{20}=4\)
\(\Rightarrow đpcm\)
2.

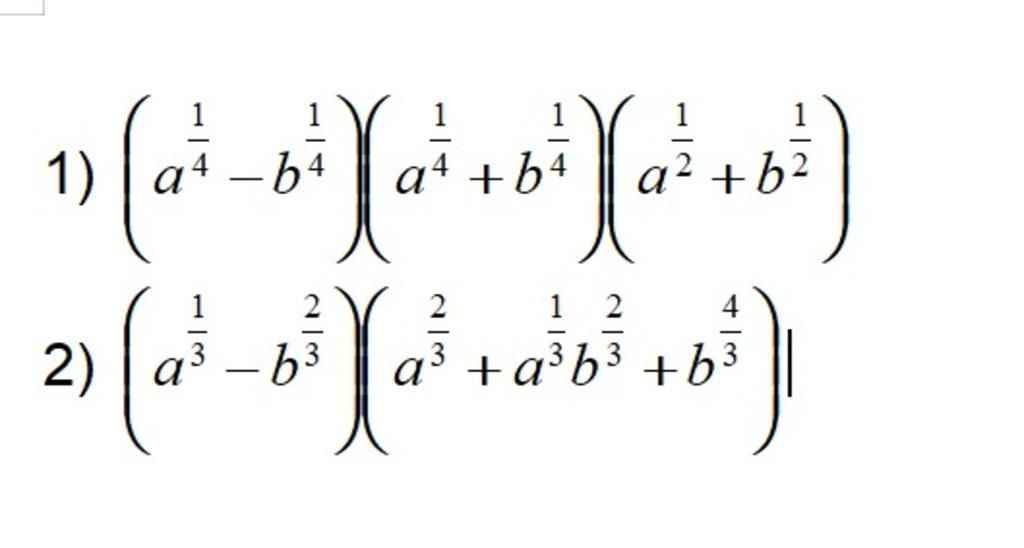
\(A=\dfrac{4^5\cdot9^4-2\cdot6^9}{2^{10}\cdot3^8+6^8\cdot20}\\ =\dfrac{\left(2^2\right)^5\cdot\left(3^2\right)^4-2\cdot2^9\cdot3^9}{2^{10}\cdot3^8+2^8\cdot3^8\cdot20}\\ =\dfrac{2^{10}\cdot3^8-2^{10}\cdot3^9}{2^{10}\cdot3^8+2^8\cdot3^8\cdot2^2\cdot5}\\ =\dfrac{2^{10}\cdot3^8-2^{10}\cdot3^9}{2^{10}\cdot3^8+2^{10}\cdot3^8\cdot5}\\ =\dfrac{2^{10}\cdot3^8\cdot\left(1-3\right)}{2^{10}\cdot3^8\cdot\left(1+5\right)}\\ =\dfrac{-2}{6}\\ =-\dfrac{1}{3}\)