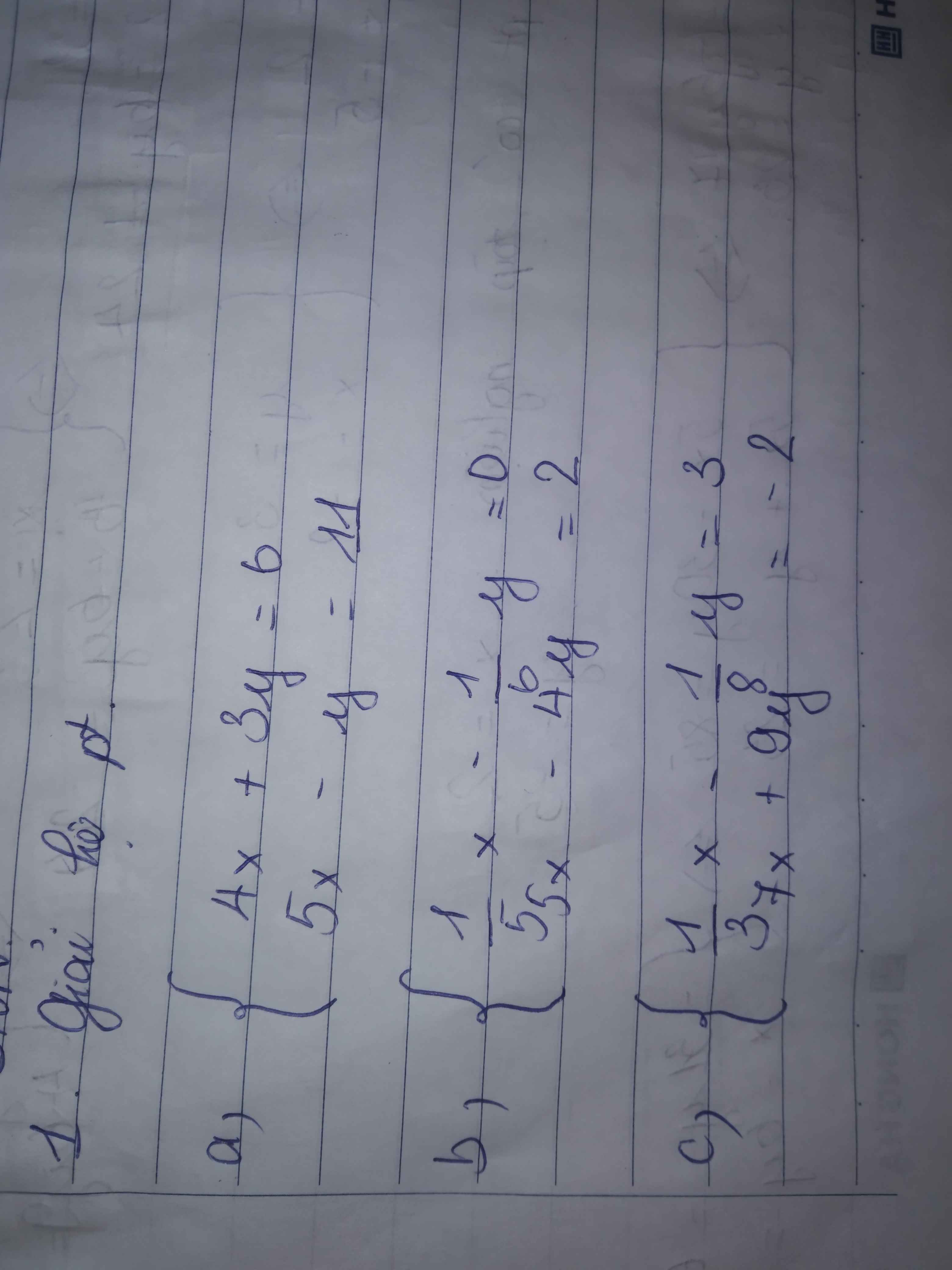
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hệ đã cho vô nghiệm bởi vì mỗi nghiệm của hệ là nghiệm chung của hai phương trình, một phương trình vô nghiệm thì hệ không có nghiệm chung.

a) Hệ đã cho vô nghiệm bởi vì mỗi nghiệm của hệ là nghiệm chung của hai phương trình, một phương trình vô nghiệm thì hệ không có nghiệm chung.
b) Hệ đã cho có vô số nghiệm.

Hệ phương trình bậc nhất hai ẩn có dạng a x + b y = c a ' x + b ' y = c '
Đáp án A: Bậc x là bậc 2 nên loại
Đáp án B: Xuất hiện 3 ẩn x; y; z nên loại
Đáp án C: Chuyển thành hệ 3 x + 2 y = 5 x − y = 0 là hệ phương trình bậc nhất hai ẩn
Đáp án D: Xuất hiện 3 phương trình với 3 ẩn x; y; z nên loại
Đáp án:C

Bước 1: Mở trang Geoebra
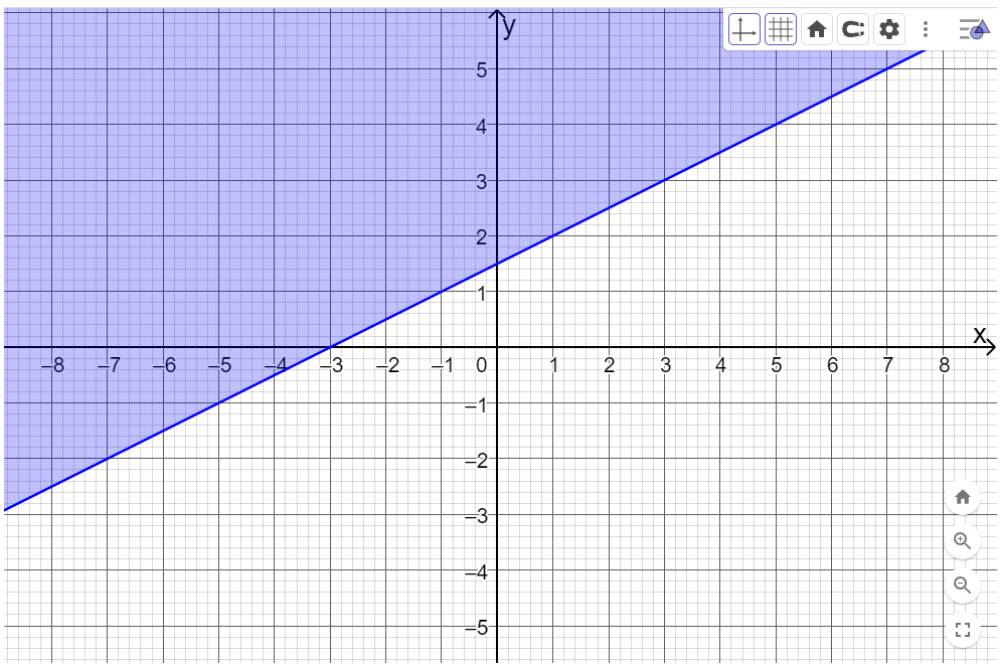
Bước 2: Nhập bất phương trình \(x - 2y + 3 \le 0\) vào ô

Và bấm enter, màn hình sẽ hiển thị như hình dưới. Miền nghiệm của bất phương trình \(x - 2y + 3 \le 0\) là miền được tô màu. Đường nét liền biểu thị miền nghiệm chứa các điểm nằm trên đường thẳng \(x - 2y + 3 = 0\).
Bước 3: Tiếp tục nhập từng bất phương trình còn lại như sau:
x+3y>-2; \(x \le 0\)(x<=0). Khi đó màn hình sẽ hiển thị như hình dưới.
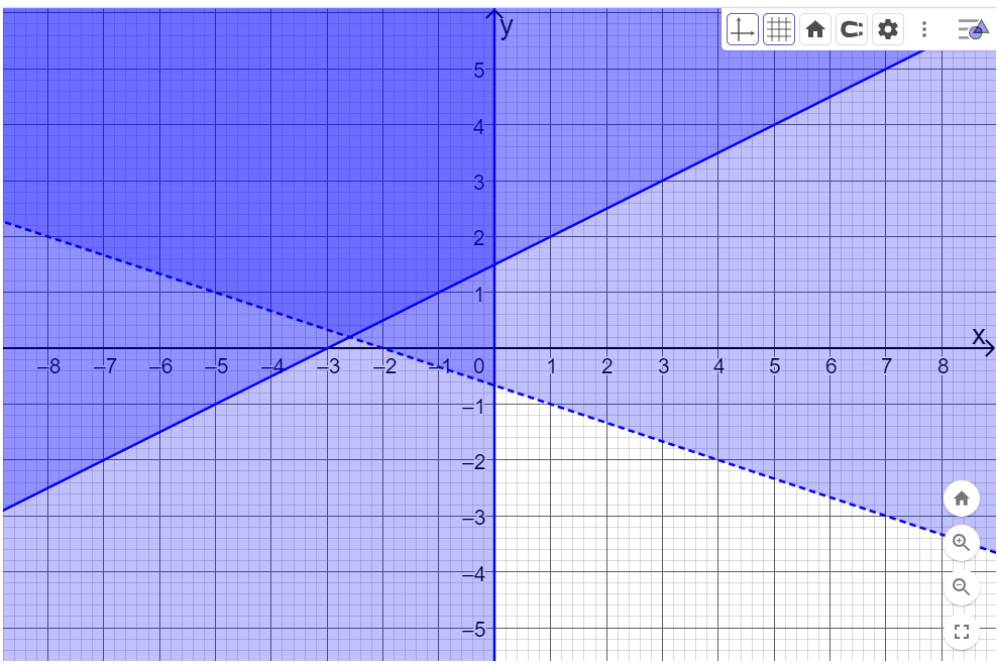
Miền nghiệm của hệ là miền được tô màu đậm nhất. Đường nét đứt biểu thị miền nghiệm không chứa các điểm nằm trên đường thẳng \(x + 3y = - 2\). Đường nét liền \(x = 0\) (trục Oy) biểu thị các điểm nằm trên trục Oy cũng thuộc miền nghiệm.

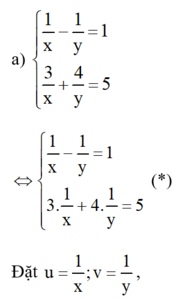
hệ phương trình (*) trở thành :
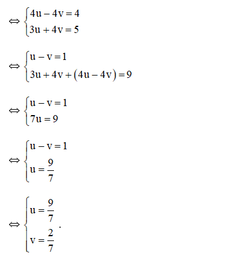
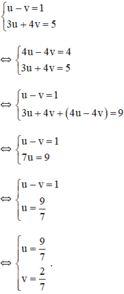
+ u = 9 7 ⇒ 1 x = 9 7 ⇒ x = 7 9 + v = 2 7 ⇒ 1 y − 2 7 ⇒ y − 7 2
Vậy hệ phương trình có nghiệm (7/9;7/2)
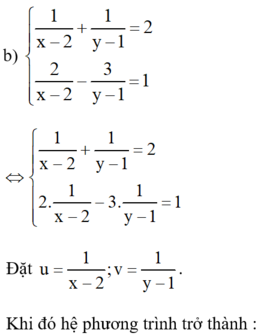
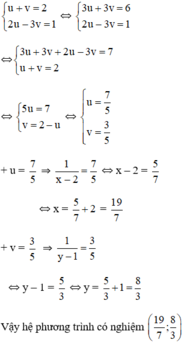
Kiến thức áp dụng
Giải hệ phương trình bằng phương pháp cộng đại số
1) Nhân hai vế của phương trình với mỗi hệ số thích hợp (nếu cần) sao cho hệ số của một trong hai ẩn bằng nhau hoặc đối nhau.
2) Áp dụng quy tắc cộng đại số để được hệ phương trình mới, trong đó có một phương trình mà hệ số của một trong hai ẩn bằng 0 (tức là phương trình một ẩn).
3) Giải phương trình một ẩn vừa thu được rồi suy ra nghiệm của hệ đã cho và kết luận.

Đáp án A
Phương án D không phải là hệ phương trình bậc nhất hai ẩn nên loại D


Hệ phương trình có chứa phương trình bậc hai là hệ phương trình ở đáp án D nên loại D
+ Với hệ phương trình A:
x − y = − 2 x + y = 4 ⇒ 1 − 3 = − 2 1 + 3 − 4 ⇔ − 2 = − 2 4 = 4 (luôn đúng) nên (1; 3) là nghiệm của hệ phương trình x − y = − 2 x + y = 4
+ Với hệ phương trình B: 2 x − y = 0 x + y = 4
Thay x = 1; y = 3 ta được 2.1 − 3 = 0 1 + 3 = 4 ⇔ − 1 = 0 1 + 3 = 4 (vô lý) nên loại B.
+ Với hệ phương trình C: x + y = 4 2 x + y = 4
Thay x = 1; y = 3 ta được 1 + 3 = 4 2.1 + 3 = 4 ⇔ 4 = 4 5 = 4 (vô lý) nên loại C.
Đáp án:A


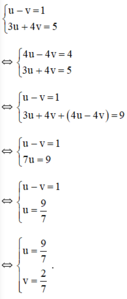

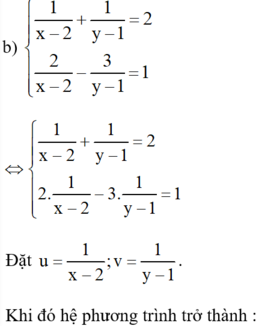
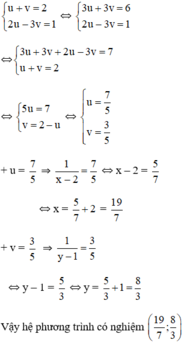
a: \(\left\{{}\begin{matrix}4x+3y=6\\5x-y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+3y=6\\15x-3y=33\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x+3y+15x-3y=6+33\\5x-y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}19x=39\\y=5x-11\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{39}{19}\\y=5\cdot\dfrac{39}{19}-11=-\dfrac{14}{19}\end{matrix}\right.\)
b: \(\left\{{}\begin{matrix}\dfrac{1}{5}x-\dfrac{1}{6}y=0\\5x-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{5}=\dfrac{y}{6}\\5x-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\5\cdot\dfrac{5}{6}y-4y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\\dfrac{25}{6}y-4y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{5}{6}y\\\dfrac{1}{6}y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=12\\x=\dfrac{5}{6}\cdot12=10\end{matrix}\right.\)
c: \(\left\{{}\begin{matrix}\dfrac{1}{3}x-\dfrac{1}{8}y=3\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{3}-\dfrac{y}{8}=3\\7x+9y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{8x-3y}{24}=3\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}8x-3y=72\\7x+9y=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}24x-9y=216\\7x+9y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}24x-9y+7x+9y=216-2\\8x-3y=72\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}31x=214\\3y=8x-72\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{214}{31}\\y=\dfrac{8x-72}{3}=\dfrac{-520}{93}\end{matrix}\right.\)
mọi người giúp e với ạ