CHỨNG MINH H NẰM GIỮA HAI ĐIỂM B VÀ C
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 11 2017
Theo ví dụ 2, ta có: A'B'→ = tA'C'→
Mà 0 < t < 1 ⇒ B' nằm giữa A' và C'
CM
22 tháng 3 2018
a) Chứng minh tứ giác ABOC nội tiếp được đường tròn.
A B O ^ = 90 0 A C O ^ = 90 0 A B O ^ + A C O ^ = 180 0
=> tứ giác ABOC nội tiếp được đường tròn.
b) Vẽ cát tuyến ADE của (O) sao cho ADE nằm giữa 2 tia AO, AB; D, E Î (O) và D nằm giữa A, E. Chứng minh A B 2 = A D . A E .
Tam giác ADB đồng dạng với tam giác ABE
⇒ A B A E = A D A B ⇔ A B 2 = A D . A E
c) Gọi F là điểm đối xứng của D qua AO, H là giao điểm của AO và BC. Chứng minh: ba điểm E, F, H thẳng hàng.
Ta có D H A ^ = E H O ^
nên D H A ^ = E H O ^ = A H F ^ ⇒ A H E ^ + A H F ^ = 180 0 ⇒ 3 điểm E, F, H thẳng hàng.
19 tháng 5 2022
Có 1 phần câu trả lời ở đây.
Giải toán: Bài hình trong đề thi HK2 Lớp 9 | Rất phức tạp. - YouTube
10 tháng 5 2023
d: CK/AD=CB/AB
=>AD*CB=CK*AB=AB*DK
=>DK/CB=AD/AB
=>ΔBCA đồng dạng với ΔDKA
=>góc BAC=góc DAK
AM vuông góc OA
EF vuông góc OA
=>AM//EF
=>góc AEF=góc MAC=góc ADC
=>ΔADC đồng dạng với ΔAEF
=>CD/EF=AD/AE
góc EAH=góc KAD; góc AEH=góc ADK
=>ΔAEH đồng dạng với ΔADK
=>DK/EH=AD/AE
=>CD/EF=DK/EH
=>EH=FH
5 tháng 2 2023
a: \(CA=\sqrt{\left(2R\right)^2-R^2}=R\sqrt{3}\)
b: Xét ΔCAD và ΔCEA có
góc CAD=góc CEA
góc ACD chung
=>ΔCAD đồng dạng vơi ΔCEA
=>CA/CE=CD/CA
=>CA^2=CE*CD
c: Xét (O) có
CA,CB là tiếp tuýen
nên CA=CB
mà OA=OB
nên OC là trung trực của AB
=>OC vuông góc AB
=>CH*CO=CA^2=CD*CE
=>CH/CE=CD/CO
=>ΔCHD đồng dạng với ΔCEO
=>góc CDH=góc COE
CM
21 tháng 4 2019
Áp dụng định nghĩa: phép dời hình là phép biến hình bảo toàn khoảng cảnh giữa hai điểm bất kỳ
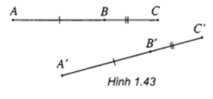
Nên ảnh của 3 điểm A, B, C qua phép dời hình F là 3 điểm A', B', C'
Khi đó:
AB = A'B', BC = B'C', AC = A'C'
Ta có: A, B, C thằng hàng và B nằm giữa A và C ⇒ AB + BC = AC
⇒ A'B' + B'C' = A'C'
Hay A', B', C' thẳng hàng và B' nằm giữa A' và C'
Vì H nằm trên cùng 1 đoạn thẳng BC Và hai đầu mút là B và C còn H nằm giữa nên H nằm giữa A vàB
nhìn hình là biết rồi cha nội