K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 12 2017
Đáp án B
Phương pháp : Chia hai trường hợp :
TH1 : Học sinh TWO làm được 2 trong số 3 bài trong đề thi.
TH2 : Học sinh TWO làm được cả 3 bài trong đề thi.
Cách giải : Ω = C 2 n 3
TH1 : Học sinh TWO làm được 2 trong số 3 bài trong đề thi. Có C n 2 . C n 1 cách
TH2 : Học sinh TWO làm được cả 3 bài trong đề thi. Có C n 3 cách
Gọi A là biến cố học sinh TWO không phải thi lại
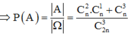
Đến đây chọn một giá trị bất kì của n rồi thay vào là nhanh nhất, chọn n =10 , ta tính được P ( A ) = 1 2
10 tháng 5 2022
1: Bài toán tính tổng tích
Input: a,b
Output: a+b và a-b
Mô tả thuật toán
Bước 1: Nhập a,b
Bước 2: Xuất a+b và a-b
Bước 3: Kết thúc
CH
11 tháng 5 2022
1: Bài toán tính tổng tích
Input: a,b
Output: a+b và a-b
Mô tả thuật toán
Bước 1: Nhập a,b
Bước 2: Xuất a+b và a-b
Bước 3: Kết thúc
HQ
Hà Quang Minh
Giáo viên
1 tháng 10 2023
\(\Omega \) là tập tất cả 6 học sinh trong 12 học sinh. Vậy \(n\left( \Omega \right) = C_{12}^6 = 924\).
Gọi C là biến cố: “Có 3 học sinh nam và 3 học sinh nữ”. Có \(C_7^3\) cách chọn chọn 3 học sinh nam và \(C_5^3\) cách chọn 3 học sinh nữ. Theo quy tắc nhân, ta có \(C_7^3.C_5^3 = 350\) cách chọn 3 học sinh nam và 3 học sinh nữ tức là \(n\left( C \right) = 350\).Vậy \(P\left( C \right) = \frac{{350}}{{924}} \approx 0,3788\).
Bài 1:
Gọi số lập được có dạng là \(\overline{abc}\)
c có 3 cách chọn
a có 6 cách chọn
b có 5 cách chọn
Do đó: Có \(3\cdot6\cdot5=90\left(số\right)\) lập được
Số số tự nhiên có 3 chữ số phân biệt lập được là \(7\cdot6\cdot5=210\left(số\right)\)
Xác suất để số được chọn là số chẵn là \(\dfrac{90}{210}=\dfrac{3}{7}\)
Bài 2:
Số cách chọn ngẫu nhiên 4 quả cầu là: \(C^4_{10}\)
Số cách chọn 4 quả cầu trắng là: \(C^4_4\)(cách)
Số cách chọn 4 quả cầu xanh là \(C^4_6\left(cách\right)\)
Xác suất để chọn được 4 quả cầu cùng màu là:
\(\dfrac{C_4^4+C_6^4}{C_{10}^4}=\dfrac{8}{105}\)