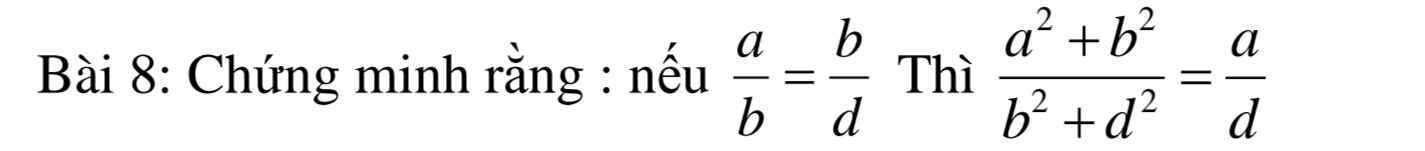 giải giúp mình với mình đang cần gấp ai giải đc mình tick cho
giải giúp mình với mình đang cần gấp ai giải đc mình tick cho
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+ đại lượng tỉ lệ nghịch: y = \(\frac{a}{x}\)
+ đại lượng tỉ lệ thuận: y = a.x
t i c k nhé 45657

Gọi hai số cần tìm là \(a,b\)
\(\Rightarrow\frac{a}{b}=\frac{10}{15}=\frac{2}{3}\Rightarrow\frac{a}{2}=\frac{b}{3}\) và \(a+b=222,5\)
Áp dụng tính chất của dảy tỉ số bằng nhau ta có:
\(\frac{a}{2}=\frac{b}{3}=\frac{a+b}{2+3}=\frac{222,5}{5}=44,5\)
\(\Rightarrow\frac{a}{2}=44,5\Rightarrow a=44,5.2=89\)
\(\Rightarrow\frac{b}{3}=44,5\Rightarrow b=44,5.3=133,5\)

\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}=\frac{2b}{2d}=\frac{a-2b}{c-2d}\)
\(\Rightarrow\frac{b}{d}=\frac{a-2b}{c-2d}\)
\(\Rightarrow\frac{a-2b}{b}=\frac{c-2d}{d}\)
Đặt \(\frac{a}{b}=\frac{c}{d}=K\)
\(\Rightarrow a=Kb\)và \(c=Kd\)
\(\frac{a-2b}{b}=\frac{Kb-2b}{b}=\frac{b\left(K-2\right)}{b}=K-2\)
\(\frac{c-2d}{d}=\frac{Kd-2d}{d}=\frac{d\left(K-2\right)}{d}=K-2\)
Vậy\(\frac{a-2b}{b}=\frac{c-2d}{d}\)

1.
a) Hai đại lượng x, y tỉ lệ thuận với nhau
b)Hai đại lượng x, y không tỉ lệ thuận với nhau

a, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}=\dfrac{a-b}{c-d}\Rightarrow\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
b, Áp dụng t/c dtsbn:
\(\dfrac{a}{b}=\dfrac{c}{d}\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{2a}{2c}=\dfrac{5b}{5d}=\dfrac{3a}{4c}=\dfrac{4b}{4d}=\dfrac{2a+5b}{2c+5d}=\dfrac{3a-4b}{3c-4d}\Rightarrow\dfrac{2a+5b}{3a-4b}=\dfrac{2c+5d}{3c-4d}\)
c, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Ta có \(\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot d}=\dfrac{b^2k}{d^2k}=\dfrac{b^2}{d^2}\)
\(\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}=\dfrac{\left(bk-b\right)^2}{\left(dk-d\right)^2}=\dfrac{b^2\left(k-1\right)^2}{d^2\left(k-1\right)^2}=\dfrac{b^2}{d^2}\)
Do đó \(\dfrac{ab}{cd}=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\)
d, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
Ta có \(\dfrac{ac}{bd}=\dfrac{bk\cdot dk}{bd}=k^2\)
\(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{b^2k^2+d^2k^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\)
Do đó \(\dfrac{ac}{bd}=\dfrac{a^2+c^2}{b^2+d^2}\)
\(\dfrac{a}{b}=\dfrac{b}{d}=>b^2=ad\)
Ta có:
\(VT=\dfrac{a^2+b^2}{b^2+d^2}=\dfrac{a^2+ad}{ad+d^2}=\dfrac{a\left(a+d\right)}{d\left(a+d\right)}=\dfrac{a}{d}=VP\)