các bạn giúp mình dzới
cho các số nguyên dương a,b,c thoả mãn a2 + ab = c2. Chứng minh rằng 2a + b + 2c là hợp số.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NN
Nga Nguyễn Thị Thanh
24 tháng 6
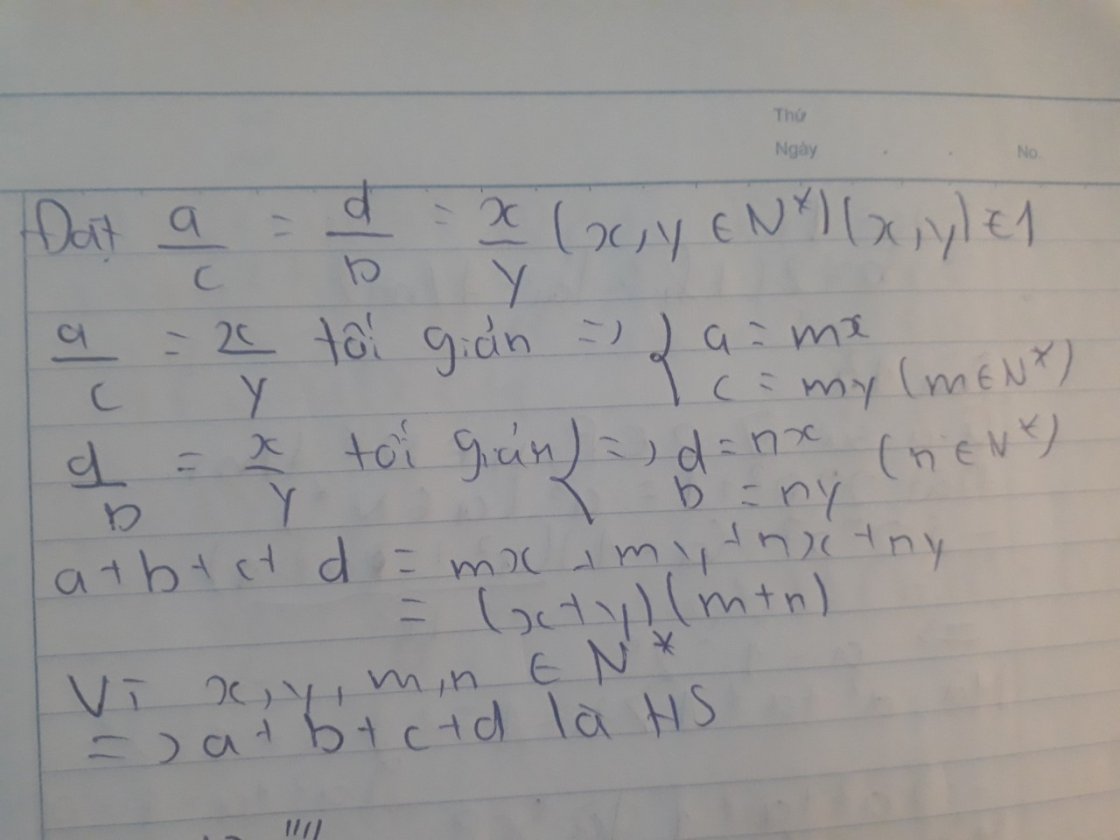Bạn vt lại gt lại \(a\left(a+b\right)=c^2\) bạn áp dụng bổ đề trên ta được a+a+b+c+c là hợp số
Đúng(0)
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 2 2021
Đặt \(P=a^2+b^2+c^2+ab+bc+ca\)
\(P=\dfrac{1}{2}\left(a+b+c\right)^2+\dfrac{1}{2}\left(a^2+b^2+c^2\right)\)
\(P\ge\dfrac{1}{2}\left(a+b+c\right)^2+\dfrac{1}{6}\left(a+b+c\right)^2=6\)
Dấu "=" xảy ra khi \(a=b=c=1\)
T
15 tháng 5 2019
Cân bằng hệ số:
Giả sư: \(2a^2+ab+2b^2=x\left(a+b\right)^2+y\left(a-b\right)^2\) (ta đi tìm x ; y)
\(=xa^2+x.2ab+xb^2+ya^2-y.2ab+yb^2\)
\(=\left(x+y\right)a^2+2\left(x-y\right)ab+\left(x+y\right)b^2\)
Đồng nhất hệ số ta được: \(\hept{\begin{cases}x+y=2\\2\left(x-y\right)=1\end{cases}\Leftrightarrow}\hept{\begin{cases}2x+2y=4\\2x-2y=1\end{cases}}\Leftrightarrow4x=5\Leftrightarrow x=\frac{5}{4}\Leftrightarrow y=\frac{3}{4}\)
Do vậy: \(2a^2+ab+2b^2=\frac{5}{4}\left(a+b\right)^2+\frac{3}{4}\left(a-b\right)^2\ge\frac{5}{4}\left(a+b\right)^2\)
Tương tự với hai BĐT còn lại,thay vào,thu gọn và đặt thừa số chung,ta được:
\(VT\ge\sqrt{\frac{5}{4}}.2.\left(a+b+c\right)=\sqrt{\frac{5}{4}}.2.3=3\sqrt{5}\) (đpcm)
Dấu "=" xảy ra khi a = b =c = 1
30 tháng 8 2021
\(VT=\sqrt{\dfrac{a^2b^2}{c\left(a+b+c\right)+ab}}+\sqrt{\dfrac{b^2c^2}{a\left(a+b+c\right)+bc}}+\sqrt{\dfrac{a^2c^2}{b\left(a+b+c\right)+ac}}\\ VT=\sqrt{\dfrac{a^2b^2}{ac+ab+bc+c^2}}+\sqrt{\dfrac{b^2c^2}{a^2+ac+ab+bc}}+\sqrt{\dfrac{a^2c^2}{ab+bc+b^2+ac}}\\ VT=\sqrt{\dfrac{a^2b^2}{\left(c+a\right)\left(b+c\right)}}+\sqrt{\dfrac{a^2c^2}{\left(b+c\right)\left(a+b\right)}}+\sqrt{\dfrac{b^2c^2}{\left(a+b\right)\left(a+c\right)}}\)
Áp dụng BĐT Cauchy-Schwarz:
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{\dfrac{b^2c^2}{\left(a+b\right)\left(a+c\right)}}\le\dfrac{\dfrac{bc}{a+b}+\dfrac{bc}{a+c}}{2}\\\sqrt{\dfrac{a^2c^2}{\left(a+b\right)\left(b+c\right)}}\le\dfrac{\dfrac{ca}{a+b}+\dfrac{ca}{b+c}}{2}\\\sqrt{\dfrac{a^2b^2}{\left(b+c\right)\left(a+c\right)}}\le\dfrac{\dfrac{ab}{b+c}+\dfrac{ab}{a+c}}{2}\end{matrix}\right.\)
\(\Rightarrow VT\le\dfrac{\left(\dfrac{bc}{a+b}+\dfrac{ca}{a+b}\right)+\left(\dfrac{ca}{b+c}+\dfrac{ab}{b+c}\right)+\left(\dfrac{bc}{a+c}+\dfrac{ab}{a+c}\right)}{2}\\ \Rightarrow VT\le\dfrac{a+b+c}{2}=\dfrac{2}{2}=1\)
Dấu \("="\Leftrightarrow a=b=c=\dfrac{2}{3}\)
CM
23 tháng 11 2020
1)
Ta có: \(M=\Sigma_{cyc}\frac{\sqrt{3}\left(a+b+4c\right)}{\sqrt{3\left(a+b\right)\left(a+b+4c\right)}}\ge\Sigma_{cyc}\frac{\sqrt{3}\left(a+b+4c\right)}{\frac{3\left(a+b\right)+\left(a+b+4c\right)}{2}}=\Sigma_{cyc}\frac{\sqrt{3}\left(a+b+4c\right)}{2\left(a+b+c\right)}=3\sqrt{3}\)
Dấu "=" xảy ra khi a=b=c
CM
24 tháng 11 2020
2)
\(\Sigma_{cyc}\sqrt[3]{\left(\frac{2a}{ab+1}\right)^2}=\Sigma_{cyc}\frac{2a}{\sqrt[3]{2a\left(ab+1\right)^2}}\ge\Sigma_{cyc}\frac{2a}{\frac{2a+\left(ab+1\right)+\left(ab+1\right)}{3}}=3\Sigma_{cyc}\frac{a}{ab+a+1}\)
Ta có bổ đề: \(\frac{a}{ab+a+1}+\frac{b}{bc+b+1}+\frac{c}{ca+c+1}=1\left(abc=1\right)\)
\(\Rightarrow\Sigma_{cyc}\sqrt[3]{\left(\frac{2a}{ab+1}\right)^2}\ge3\)
CM
22 tháng 6 2018
Ta chứng minh BĐT
( a + b + c ) ( 1 a + 1 b + 1 c ) ≥ 9 ( * ) ( * ) < = > 3 + ( a b + b a ) + ( b c + c b ) + ( c a + a c ) ≥ 9
Áp dụng BĐT Cô – si cho hai số dương ta có:
a b + b a ≥ 2 b c + c b ≥ 2 c a + a c ≥ 2 =>(*) đúng
= > 9 a + b + c ≤ 1 a + 1 b + 1 c ≤ 3 = > a + b + c ≥ 3
Trở lại bài toán: Áp dụng BĐT Cô si cho hai số dương ta có 1 + b 2 ≥ 2 b
Ta có: a 1 + b 2 = a − a b 2 1 + b 2 ≥ a − a b 2 2 b = a − a b 2 ( 1 )
Tương tự ta có:
b 1 + c 2 ≥ b − b c 2 ( 2 ) c 1 + a 2 ≥ c − c a 2 ( 3 )
Cộng từng vế của (1), (2) và (3) ta có:
a 1 + b 2 + b 1 + c 2 + c 1 + a 2 ≥ a + b + c − 1 2 ( a b + b c + c a ) = > a 1 + b 2 + b 1 + c 2 + c 1 + a 2 + 1 2 ( a b + b c + c a ) ≥ a + b + c ≥ 3