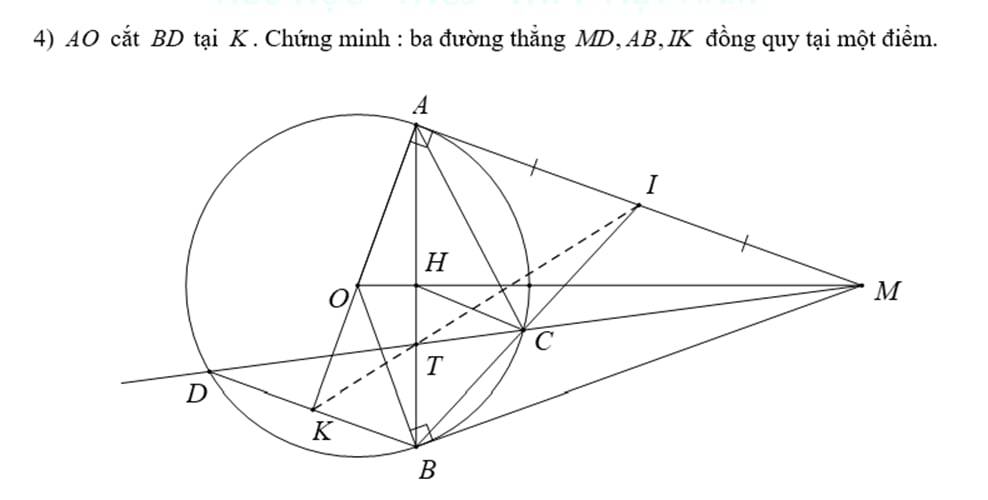
Em nhờ các thầy cô giúp em ý thứ 4 ạ. Bài tập toán 9 ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
TN
1
Những câu hỏi liên quan
19 tháng 4 2022
Xét p=2\(\Rightarrow p^4+29=45=3^2.5\), có 6 ước số là SND, loại
Xét p=3\(\Rightarrow p^4+29=110=2.5.11\), có 8 ước số là SND, tm
Xét p=5\(\Rightarrow p^4+29=654=2.3.109\) , có 8 ước số là SND, tm
Xét p\(\ge6\). Do p là SNT nên p có dạng \(6k+1\) hoặc \(6k-1\) (k\(\in N\)*)
TH1: p=6k+1
Khi đó ta có \(p^4+29=\left(6k+1\right)^4+29\equiv1+29\equiv0\left(mod6\right)\)
Ta cũng có: \(p^4+29=\left(6k+1\right)^4+29\equiv0\left(mod5\right)\)
vì \(\left(6k+1\right)⋮5̸\)
\(\Rightarrow p^4+29=6.5.a=2.3.5.a\)(a là STN)\(\Rightarrow p^4+29\) có nhiều hơn 8 ước số nguyên dương, loại.
TH2: p=6k-1. Chứng minh tương tự ta thấy không có p thoả mãn
\(\Rightarrow p\ge6\) không thoả mãn
Vậy....
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 4 2022
\(\Leftrightarrow4.25^x-4.5^x+1=4y^4+8y^3+12y^2+16y+41\)
\(\Leftrightarrow\left(2.5^x-1\right)^2=4y^4+8y^3+12y^2+16y+41\)
Ta có:
\(4y^4+8y^3+12y^2+16y+41=\left(2y^2+2y+2\right)^2+8y+37>\left(2y^2+2y+2\right)^2\)
\(4y^4+8y^3+12y^2+16y+41=\left(2y^2+2y+5\right)^2+4\left(y-1\right)\left(3y+4\right)\ge\left(2y^2+2y+5\right)^2\)
\(\Rightarrow\left[{}\begin{matrix}4y^4+8y^3+12y^2+16y+41=\left(2y^2+2y+3\right)^2\\4y^4+8y^3+12y^2+16y+41=\left(2y^2+2y+4\right)^2\\4y^4+8y^3+12y^2+16y+41=\left(2y^2+2y+5\right)^2\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}y^2-y-8=0\left(\text{không có nghiệm nguyên}\right)\\8y^2-25=0\left(\text{không có nghiệm nguyên}\right)\\\left(y-1\right)\left(3y+4\right)=0\end{matrix}\right.\)
\(\Rightarrow y=1\)
Thế vào pt ban đầu: \(25^x-5^x=20\)
Đặt \(5^x=t>0\Rightarrow t^2-t-20=0\Rightarrow\left[{}\begin{matrix}t=5\\t=-4\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow5^x=5\Rightarrow x=1\)
NQ
0
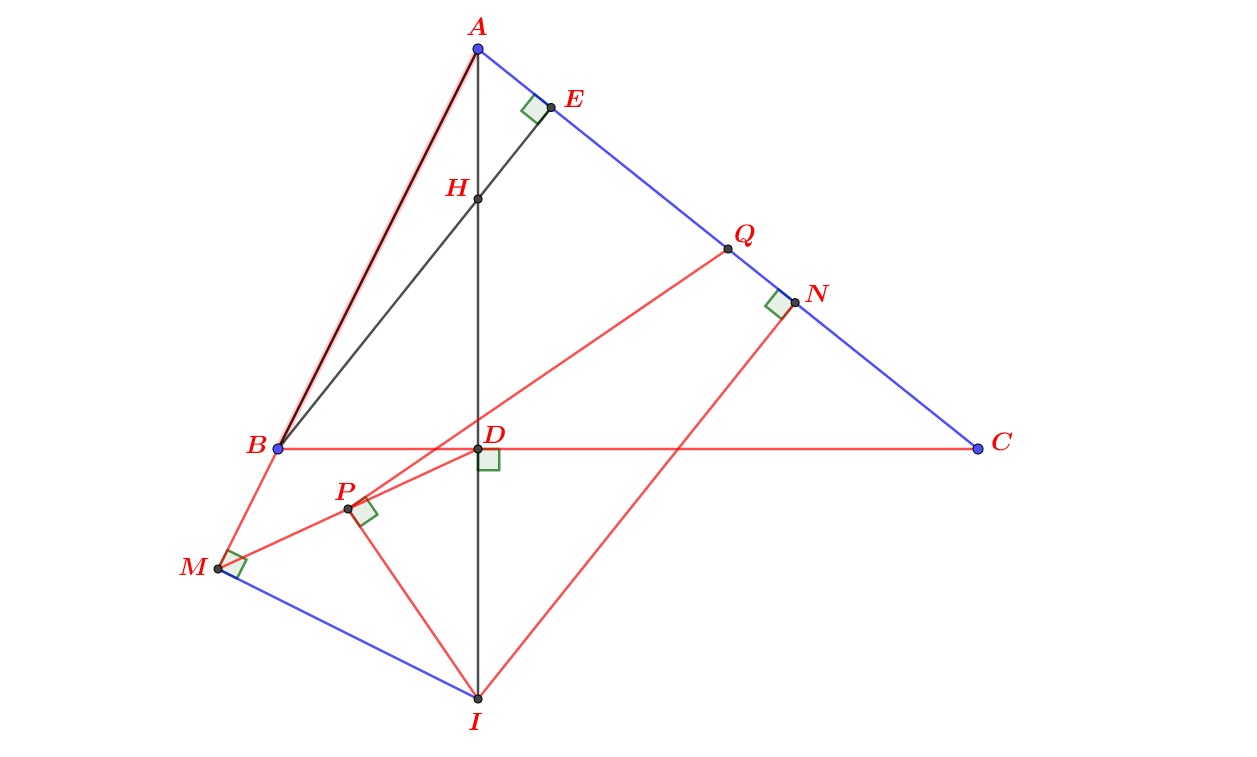
4)
Ta có:
AM // BD (cmt)
AO ⊥ AM (do MA là tiếp tuyến của (O) tại A)
⇒ AO ⊥ BD tại K
⇒ K là trung điểm của BD
Áp dụng định lý Thales đảo vào ∆AMT và ∆TBD, ta có:
⇒ ∆ATI ∽ ∆BTK (c-g-c)
⇒ ∠ATI = ∠BTK
⇒ ∠ATI và ∠BTK đối đỉnh
⇒ I, T, K thẳng hàng
⇒ T ∈ IK
⇒ MD, AB, IK đồng quy tại T