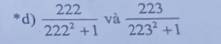
So sánh số hữu tỉ ạ em cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giống:
- Đều có tư cách pháp nhân;
- Có nhiều chủ sở hữu;
- Các thành viên chịu trách nhiệm hữu hạn đối với các khoản nợ và nghĩa vụ tài chính của công ty;
- Số vốn góp không đủ và không đúng hạn được coi là khoản nợ đối với công ty.
Khác:
Công ti TNHH
- Tối thiểu là 02 thành viên và tối đa là 50 thành viên.
- Vốn điều lệ không chia thành các phần bằng nhau
- Góp đủ và đúng loại tài sản như đã cam kết trong thời hạn 90 ngày, kể từ ngày được cấp Giấy chứng nhận đăng ký doanh nghiệp. Chỉ được góp bằng tài sản khác nếu được sự tán thành của đa số thành viên còn lại.
- Không được phát hành cố phiếu
- Chuyển nhượng phải có điều kiện (ưu tiên chuyển nhượng cho thành viên công ty).
Công ti cổ phần:
-Tối thiểu là 03 thành viên và không giới hạn tối đa.
-Vốn điều lệ chia thành các phần bằng nhau, được ghi nhận bằng cổ phiếu.
-Góp đủ số vốn đã đăng ký góp trong thời hạn 90 ngày kể từ ngày công ty được cấp Giấy chứng nhận đăng ký doanh nghiệp. Các cổ đông sáng lập phải cùng nhau đăng ký mua ít nhất 20% tổng số cổ phần phổ thông được quyền chào bán tại thời điểm đăng ký doanh nghiệp.
-Được phát hành cổ phiếu, trái phiếu
-Dễ dàng, tự do chuyển nhượng (trừ trong 03 năm đầu, cổ đông sáng lập chỉ được chuyển nhượng cổ phần cho cổ đông sáng lập khác và cho người khác không phải là cổ đông sáng lập khi được sự chấp thuận của Đại hội đồng cổ đông)

a: -1/200<0<1/2000
b; -1789/1788<-1
-1<2009/-2010
=>-1789/1788<-2009/2010
d: -27/45=-3/5
-272727/454545=-3/5
=>-27/45=-272727/454545

a: \(-\dfrac{15}{20};\dfrac{24}{-32};-\dfrac{27}{36}\)


mình gợi ý nhé 1
1. là so sánh với 1
2 . so sánh với 0
3 . rút gọn đi rồi quy đồng lên sau đó so sánh


Ta có:
\(1-\frac{175}{176}=\frac{1}{176}\)
\(1-\frac{2008}{2009}=\frac{1}{2009}\)
Vì \(\frac{1}{2009}< \frac{1}{176}\)
Do đó\(\frac{2008}{2009}< \frac{175}{176}\)

Đặt 222=a
=>\(\dfrac{222}{222^2+1}=\dfrac{a}{a^2+1};\dfrac{223}{223^2+1}=\dfrac{\left(a+1\right)^2}{\left(a+1\right)^2+1}\)
\(\dfrac{a^2}{a^2+1}-\dfrac{\left(a+1\right)^2}{\left(a+1\right)^2+1}\)
\(=\dfrac{a^2\left[\left(a+1\right)^2+1\right]-\left(a+1\right)^2\left(a^2+1\right)}{\left(a^2+1\right)\left[\left(a+1\right)^2+1\right]}\)
\(=\dfrac{a^2\left(a^2+2a+2\right)-\left(a^2+2a+1\right)\left(a^2+1\right)}{\left(a^2+1\right)\left[\left(a+1\right)^2+1\right]}\)
\(=\dfrac{a^4+2a^3+2a^2-a^4-a^2-2a^3-2a-a^2-1}{\left(a^2+1\right)\left[\left(a+1\right)^2+1\right]}\)
\(=\dfrac{-2a-1}{\left(a^2+1\right)\left[\left(a+1\right)^2+1\right]}< 0\)
=>\(\dfrac{222}{222^2+1}< \dfrac{223}{223^2+1}\)