 ai làm giúp mình câu tìm Y với
ai làm giúp mình câu tìm Y với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(y+y\div0.25+y\div0,125+y\times2=15\)
\(y\times1+y\times4+y\times8+y\times2=15\)
\(y\times\left(1+4+8+2\right)=15\)
\(y\times15=15\)
\(y=15\div15\)
\(y=1\)
y + y : 0,25 + y : 0,125 + y x 2 = 15
y x 1 + y x 4 + y x 8 + y x 2 = 15
y x (1+4+8+2) = 15
y x 15 = 15
y = 15 : 15
y = 1

\(xy+x+y=4\\ x\left(y+1\right)+y+1=4+1=5\\ \left(x+1\right)\left(y+1\right)=5\)
| \(x+1\) | \(5\) | \(1\) | \(-1\) | \(-5\) |
| \(y+1\) | \(1\) | \(5\) | \(-5\) | \(-1\) |
| \(x\) | \(4\) | \(0\) | \(-2\) | \(-6\) |
| \(y\) | \(0\) | \(4\) | \(-6\) | \(-2\) |

Bài 2:
Ta có: \(3n^3+10n^2-5⋮3n+1\)
\(\Leftrightarrow3n^3+n^2+9n^2+3n-3n-1-4⋮3n+1\)
\(\Leftrightarrow3n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
\(\Leftrightarrow3n\in\left\{0;-3;3\right\}\)
hay \(n\in\left\{0;-1;1\right\}\)

1: Ta có: \(\sqrt{3x-5}=2\)
\(\Leftrightarrow3x-5=4\)
hay x=3
2: Ta có: \(\sqrt{25\left(x-1\right)}=20\)
\(\Leftrightarrow x-1=16\)
hay x=17


\(\sqrt{a^2+3}=\sqrt{a^2+ab+bc+ca}=\sqrt{\left(a+b\right)\left(a+c\right)}\le\dfrac{1}{2}\left(a+b+a+c\right)=\dfrac{1}{2}\left(2a+b+c\right)\)
Tương tự: \(\sqrt{b^2+3}\le\dfrac{1}{2}\left(a+2b+c\right)\) ; \(\sqrt{c^2+3}\le\dfrac{1}{2}\left(a+b+2c\right)\)
Cộng vế với vế:
\(VT\le\dfrac{1}{2}\left(4a+4b+4c\right)=2\left(a+b+c\right)\)

Em chỉ cần đổi số 2015 -----> 2012
Câu hỏi của Phạm Hải Yến - Toán lớp 7 - Học toán với OnlineMath

1.theo bất đẳng thức côsi ta có
\(a+b\ge2\sqrt{ab}\\ b+c\ge2\sqrt{ab}\\ c+a\ge2\sqrt{ab}\)
\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)\ge8\sqrt{ab.bc.ca}\)
\(\ge8\sqrt{a^2b^2c^2}\\ \ge8abc\)
2.\(a^4+b^2\ge2\sqrt{a^4b^2}=2a^4b^2\)
\(\dfrac{a}{a^4+b^2}\le\dfrac{a}{2a^2b}=\dfrac{1}{2ab}\)
tương tự:\(\dfrac{b}{b^4+a^2}\le\dfrac{1}{2ab}\)
\(\rightarrow\dfrac{a}{a^4+b^2}+\dfrac{b}{b^4+a^2}\le\dfrac{1}{ab}\)
dấu = xảy ra khi \(a^4=b^2\\ b^4=a^2\)\(\rightarrow a^2=b^2=1\)



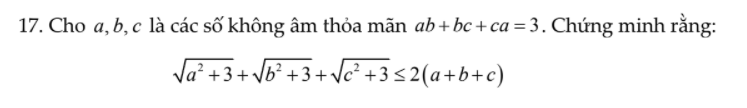 câu này với ạ! Mình cảm ơn.
câu này với ạ! Mình cảm ơn. Ai làm giúp mình câu này với ạ
Ai làm giúp mình câu này với ạ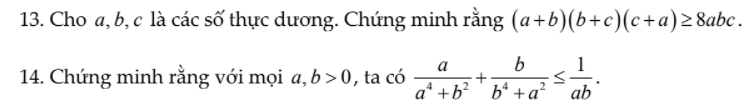

12,6 × (y - 2) - y × 5,6 = 16,8
12,6 × y - 25,2 - y × 5,6 = 16,8
y × (12,6 - 5,6) = 16,8 + 25,2
y × 7 = 42
y = 42 : 7
y = 6