Câu 14. Cho tam giác ABC có D là điểm chính giữa của cạnh BC và N là điểm chính giữa cạnh AB. Trên cạnh AC lấy điểm M sao cho AM= 1/3 x AC
a) Tính S tam giác ABC biết đáy BC dài 60cm và chiều cao hạ từ đỉnh A xuống BC dài 40 cm?
b) Tính diện tích tam giác DMN?


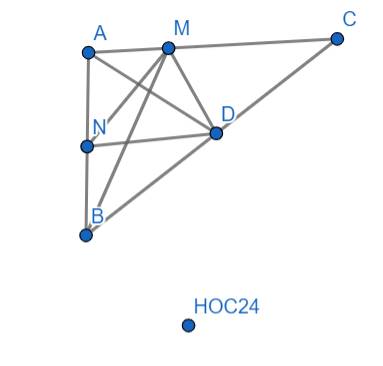
a: Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\times BC\times AH=\dfrac{1}{2}\times60\times40=1200\left(cm^2\right)\)
b: Vì \(AM=\dfrac{1}{3}AC\)
nên \(S_{ABM}=\dfrac{1}{3}\times S_{ABC}\)
Vì N là trung điểm của AB
nên \(S_{AMN}=\dfrac{1}{2}\times S_{ABM}=\dfrac{1}{6}\times S_{ABC}\)
Vì D là trung điểm của BC
nên \(S_{ADB}=S_{ADC}=\dfrac{1}{2}\times S_{ABC}\)
Vì \(AM=\dfrac{1}{3}AC\)
nên \(CM=\dfrac{2}{3}CA\)
=>\(S_{CDM}=\dfrac{2}{3}\times S_{CDA}=\dfrac{2}{3}\times\dfrac{1}{2}\times S_{ABC}=\dfrac{1}{3}\times S_{ABC}\)
Vì N là trung điểm của AB
nên \(S_{BND}=\dfrac{1}{2}\times S_{ADB}=\dfrac{1}{4}\times S_{ABC}\)
Ta có: \(S_{AMN}+S_{MDC}+S_{NBD}+S_{MND}=S_{ABC}\)
=>\(S_{MND}=S_{ABC}\left(1-\dfrac{1}{3}-\dfrac{1}{6}-\dfrac{1}{4}\right)=\dfrac{1}{4}\times S_{ABC}\)
=>\(S_{MND}=\dfrac{1}{4}\times1200=300\left(cm^2\right)\)