1 3y/13=1 5y/5x=1 4y/4y
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1) \(4x^5y^2-8x^4y^2+4x^3y^2\)
\(=4x^3y^2\left(x^2-2x+1\right)\)
\(=4x^3y^2\left(x^2-2\cdot x\cdot1+1^2\right)\)
\(=4x^3y^2\left(x-1\right)^2\)
2) \(5x^4y^2-10x^3y^2+5x^2y^2\)
\(=5x^2y^2\left(x^2-2x+1\right)\)
\(=5x^2y^2\left(x^2-2\cdot x\cdot1+1^2\right)\)
\(=5x^2y^2\left(x-1\right)^2\)
3) \(12x^2-12xy+3y^2\)
\(=3\left(4x^2-4xy+y^2\right)\)
\(=3\left[\left(2x\right)^2-2\cdot2x\cdot y+y^2\right]\)
\(=3\left(2x-y\right)^2\)
4) \(8x^3-8x^2y+2xy^2\)
\(=2x\left(4x^2-4xy+y^2\right)\)
\(=2x\left[\left(2x\right)^2-2\cdot2x\cdot y+y^2\right]\)
\(=2x\left(2x-y\right)^2\)
5) \(20x^4y^2-20x^3y^3+5x^2y^4\)
\(=5x^2y^2\left(4x^2-4xy+y^2\right)\)
\(=5x^2y^2\left[\left(2x\right)^2-2\cdot2x\cdot y+y^2\right]\)
\(=5x^2y^2\left(2x-y\right)^2\)
1: 4x^5y^2-8x^4y^2+4x^3y^2
=4x^3y^2(x^2-2x+1)
=4x^3y^2(x-1)^2
2: \(=5x^2y^2\left(x^2-2x+1\right)=5x^2y^2\left(x-1\right)^2\)
3: \(=3\left(4x^2-4xy+y^2\right)=3\left(2x-y\right)^2\)
4: \(=2x\left(4x^2-4xy+y^2\right)=2x\left(2x-y\right)^2\)
5: \(=5x^2y^2\left(4x^2-4xy+y^2\right)=5x^2y^2\left(2x-y\right)^2\)


a) \(2x\left(x-7\right)-5y\left(x-7\right)=\left(x-7\right)\left(2x-5y\right)\)
b) \(5x^3y+10x^2y+5xy=5xy\left(x^2+2x+1\right)=5xy\left(x+1\right)^2\)
c) \(4y^2-4y-x^2+1=\left(2y-1\right)^2-x^2=\left(2y-1-x\right)\left(2y-1+x\right)\)
d) \(x\left(x+1\right)\left(x+2\right)\left(x+3\right)+1=\left(x^2+3x\right)\left(x^2+3x+2\right)+1\)
\(=\left(x^2+3x\right)^2+2\left(x^2+3x\right)+1=\left(x^2+3x+1\right)^2\)
a: \(=\left(x-7\right)\left(2x-5y\right)\)
b: \(=5xy\left(x^2+2x+1\right)=5xy\left(x+1\right)^2\)

h) \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=2\\\dfrac{3}{x}-\dfrac{4}{y}=-1\end{matrix}\right.\)\(\left(1\right)\)\(\left(đk:x,y\ne0\right)\)
Đặt \(a=\dfrac{1}{x},b=\dfrac{1}{y}\)
\(\left(1\right)\Leftrightarrow\) \(\left\{{}\begin{matrix}a+b=2\\3a-4b=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}3a+3b=6\\3a-4b=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=2\\7b=7\end{matrix}\right.\)\(\Leftrightarrow a=b=1\)
Thay a,b:
\(\Leftrightarrow\dfrac{1}{x}=\dfrac{1}{y}=1\Leftrightarrow x=y=1\left(tm\right)\)

\(\left\{{}\begin{matrix}4x+5y=14\\5x+4y=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{14-5y}{4}\\\dfrac{70-25y}{4}+4y=13\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{14-5y}{4}\\\dfrac{70-9y}{4}=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{14-5y}{4}\\y=\dfrac{70-\left(13.4\right)}{9}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{14-5.2}{4}\\y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
thay x = 1 ; y=2 và 9x + 9y ta đc
\(\Leftrightarrow9+9.2=9+18=27\)

a) Ta có: \(3x-y=13\) và \(2x-4y=60\)
Mà: \(2\left(x+2y\right)=60\Rightarrow x+2y=30\) (1)
Và: \(3x-y=13\Rightarrow6x-2y=26\) (2)
Cộng (1) với (2) theo vế ta có:
\(\left(x+6x\right)+\left(-2y+2y\right)=30+26\)
\(\Rightarrow7x=56\)
\(\Rightarrow x=8\)
Ta tìm được y:
\(8+2y=30\)
\(\Rightarrow2y=22\)
\(\Rightarrow y=11\)

a, \(2x^2+3\left(x+1\right)\left(x-1\right)-5x\left(x+1\right)\)
\(=2x^2+3\left(x^2-1\right)-5x^2-5x\)
\(=2x^2+3x^2-3-5x^2-5x\)
\(=\left(2x^2+3x^2-5x^2\right)-3-5x\)
\(=-\left(5x+3\right)\)
b, \(\left(4x+3y\right)\left(2x-5y\right)-\left(2x+6y\right)\left(3x-5y\right)\)
\(=8x^2-20xy+6xy-\left(15y^2-6x^2-10xy-18xy-30y^2\right)\)
\(=8x^2-20xy+6xy-15y^2+6x^2+10xy+18xy+30y^2\)
\(=\left(8x^2+6x^2\right)+\left(-20xy+6xy+10xy+18xy\right)+\left(-15y^2+30y^2\right)\)
\(=14x^2+14xy+15y^2\)
\(=14x.\left(x+y\right)+15y^2\)
Chúc bạn học tốt!!!
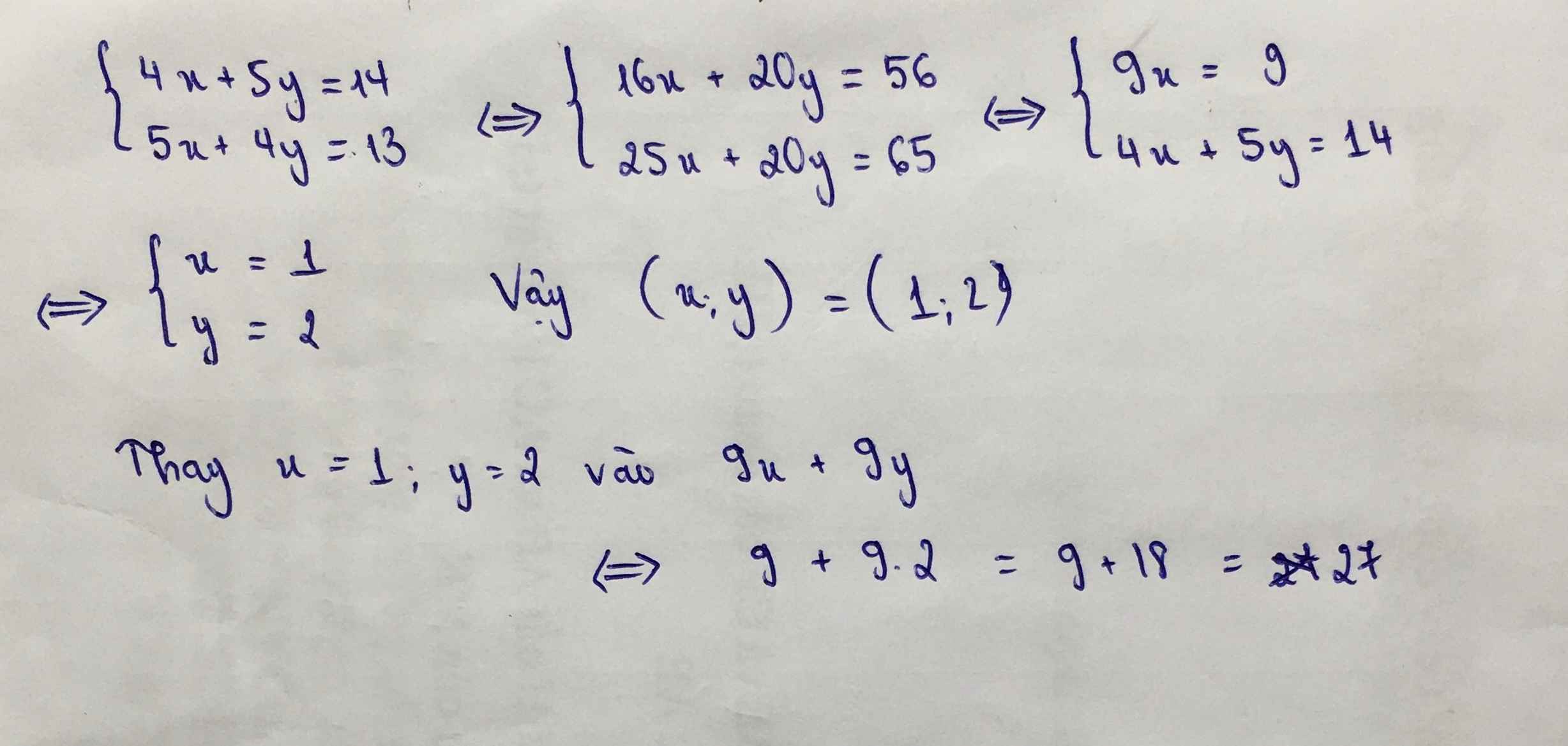
Đề đọc khó hiểu quá. Các ký hiệu thiếu tùm lum không à. Bạn xem lại nhé.