Cho ba số a,b,c khác 0, thỏa mãn (a+b+c)(1/a+1/b+1/c) = 1
Tính giá trị của biểu thức : (a^23+b^23)(b^5+c^5)(a^1995+c^1995).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
G
13 tháng 3 2019
\(\Leftrightarrow\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}\)
\(\Leftrightarrow\frac{ab+bc+ac}{abc}=\frac{1}{a+b+c}\Leftrightarrow\left(a+b+c\right)\left(ab+bc+ac\right)-abc=0\)
\(\Leftrightarrow a^2b+a^2c+b^2a+b^2c+abc+abc+bc^2+ac^2=0\)
\(\Leftrightarrow\left(a+b\right)\left(b+c\right)\left(a+c\right)=0\Leftrightarrow...\)
\(P=0\)
MH
17 tháng 9 2023
Ta có: \(a^2+1=a^2+ab+bc+ca=\left(a+b\right)\left(c+a\right)\)
Tương tự: \(\left\{{}\begin{matrix}b^2+1=\left(a+b\right)\left(b+c\right)\\c^2+1=\left(c+a\right)\left(b+c\right)\end{matrix}\right.\)
=> \(\left(a^2+1\right)\left(b^2+1\right)\left(c^2+1\right)=\left[\left(a+b\right)\left(b+c\right)\left(c+a\right)\right]^2\)
Mặt khác: \(a+b+c-abc=a\left(1-bc\right)+b+c\)
\(=a\left(ab+ca\right)+b+c\) (Vì ab+bc+ca=1)
\(=\left(a^2+1\right)\left(b+c\right)\)
\(=\left(a+b\right)\left(b+c\right)\left(c+a\right)\) (Vì \(a^2+1=\left(a+b\right)\left(c+a\right)\))
\(T=1\)
CM
27 tháng 6 2017
Gọi M a ; b ; N c ; d
Khi đó ta có M thuộc đường tròn x - 1 2 + y - 2 2 = 1 C và N thuộc đường thẳng
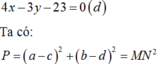
Đường tròn (C) có tâm I 1 ; 2 , bán kính R = 1
Ta có
Khi đó
Chọn D.
\(\left(a+b+c\right)\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)=1\)
\(\Leftrightarrow\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=\frac{1}{a+b+c}\)
\(\Leftrightarrow\frac{1}{a}+\frac{1}{b}=\frac{1}{a+b+c}-\frac{1}{c}\)
\(\Leftrightarrow\left(a+b\right)\left(b+c\right)\left(c+a\right)=0\)
\(\Leftrightarrow a+b=0\Leftrightarrow a=-b\)
\(\Rightarrow a^{23}+b^{23}=-b^{23}+b^{23}=0\)
Vậy \(\left(a^{23}+b^{23}\right)\left(a^{1995}+c^{1995}\right)=0\)