y=g(x)=x2-3x+1 tính g(-1),g(0),g(1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
4 tháng 4 2021
1a.
\(y'=3x^2.f'\left(x^3\right)-2x.g'\left(x^2\right)\)
b.
\(y'=\dfrac{3f^2\left(x\right).f'\left(x\right)+3g^2\left(x\right).g'\left(x\right)}{2\sqrt{f^3\left(x\right)+g^3\left(x\right)}}\)
2.
\(f'\left(x\right)=\left(m-1\right)x^3+\left(m-2\right)x^2-2mx+3=0\)
Để ý rằng tổng hệ số của vế trái bằng 1 nên pt luôn có nghiệm \(x=1\), sử dụng lược đồ Hooc-ne ta phân tích được:
\(\Leftrightarrow\left(x-1\right)\left[\left(m-1\right)x^2+\left(2m-3\right)x-3\right]=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\\left(m-1\right)x^2+\left(2m-3\right)x-3=0\left(1\right)\end{matrix}\right.\)
Xét (1), với \(m=1\Rightarrow x=-3\)
- Với \(m\ne1\Rightarrow\Delta=\left(2m-3\right)^2+12\left(m-1\right)=4m^2-3\)
Nếu \(\left|m\right|< \dfrac{\sqrt{3}}{2}\Rightarrow\) (1) vô nghiệm \(\Rightarrow f'\left(x\right)=0\) có đúng 1 nghiệm
Nếu \(\left|m\right|>\dfrac{\sqrt{3}}{2}\Rightarrow\left(1\right)\) có 2 nghiệm \(\Rightarrow f'\left(x\right)=0\) có 3 nghiệm
CM
5 tháng 5 2018
a) f(-2) = -1; f(-1) = 0; f(0) = 1; f(2) = 3
g(-1) = 0,5; g(-2) = 2; g(0) = 0
b) f(x) = 2 ⇒ x = 1
g(x) = 2 ⇒ x = 2 hoặc x = -2
CM
24 tháng 8 2017
Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:
* Ta có: f(x) = x5 – 3x2 + x3 – x2 – 2x + 5
= x5 – (3x2 + x2 ) + x3 - 2x + 5
= x5 – 4x2 + x3 – 2x + 5
= x5 + x3 – 4x2 – 2x + 5
Và g(x) = x2 – 3x + 1 + x2 – x4 + x5
= (x2 + x2 ) – 3x + 1 – x4 + x5
= 2x2 – 3x + 1 – x4 + x5
= x5 – x4 + 2x2 – 3x + 1
* f(x) + g(x):
10 tháng 8 2016
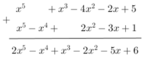
Bài 1:
\(A=x^2y-y+xy^2-x=\left(x^2y+xy^2\right)-\left(x+y\right)\\ =xy\left(x+y\right)-\left(x+y\right)=\left(x+y\right)\left(xy-1\right)\)
Voqis x=-1;y=3 ta có:
\(A=\left(-1+3\right)\left(-1\cdot3-1\right)=2\cdot\left(-4\right)=-8\)
b) \(B=x^2y^2+xy+x^3+y^3=\left(x^2y^2+x^3\right)+\left(xy+y^3\right)\\ =x^2\left(y^2+x\right)+y\left(x+y^2\right)=\left(x+y^2\right)\left(x^2+y\right)\)
Với x=-1;y=3 ta có:
\(B=\left(-1+3^2\right)\left(-1^2+3\right)=8\cdot2=16\)
c) \(C=2x+xy^2-x^2y-2y=\left(2x-2y\right)+\left(xy^2-x^2y\right)\\ =2\left(x-y\right)+xy\left(y-x\right)=\left(x-y\right)\left(2-xy\right)\)
Với x=-1;y=3 ta có:
\(C=\left(-1-3\right)\left(2-\left(-1\right)\cdot3\right)=-4\cdot5=-20\)
d) phân tích tt
15 tháng 8 2021
a: \(F\left(x\right)=x^5-3x^2+x^3-x^2-2x+5\)
\(=x^5+x^3-4x^2-2x+5\)
\(G\left(x\right)=x^5-x^4+x^2-3x+x^2+1\)
\(=x^5-x^4+2x^2-3x+1\)
b: Ta có: \(H\left(x\right)=F\left(x\right)+G\left(x\right)\)
\(=x^5+x^3-4x^2-2x+5+x^5-x^4+2x^2-3x+1\)
\(=2x^5-x^4+x^3-2x^2-5x+6\)
\(g\left(-1\right)=\left(-1\right)^2-3.\left(-1\right)+1=5\)
\(g\left(0\right)=0^2-3.0+1=1\)
\(g\left(1\right)=1^2-3.1+1=-1\)
\(g_{\left(-1\right)}=\left(-1\right)^2-3\cdot\left(-1\right)+1=1+3+1=5\)
\(g_{\left(0\right)}=0^2-3\cdot0+1=0-0+1=1\)
\(g_{\left(1\right)}=1^2-3\cdot1+1=1-3+1=-1\)