cho tam giac ABC vuông cân tại A , AC = 4cm . điểm M thuộc BC . Gọi D,E theo thứ tự là chân các dường vuông góc kẻ từ M đến AB, AC Điển M ở vị trí nào trên cạnh BC thì đoạn DE có độ dài nhỏ nhất
ai giai nhanh minh tick cho 2 cai nhé
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 1 2018
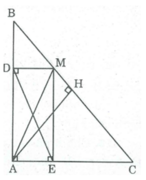
Gọi H là trung điểm của BC
Suy ra: AH ⊥ BC (tính chất tam giác cân)
Do đó, AM ≥ AH ( quan hệ đường vuông góc và đường xiên )(dấu " = " xảy ra khi M trùng với H)
Tứ giác ADME là hình chữ nhật .
⇒ AM = DE (tính chất hình chữ nhật)
Suy ra: DE ≥ AH
Vậy DE có độ dài nhỏ nhất là AH khi và chỉ khi điểm M là trung điểm của BC.
30 tháng 6 2017
Ta có \(DE=AM\ge AH\). Dấu " = " xảy ra khi \(M\equiv H\)
Vậy DE có độ dài nhỏ nhất là AH khi điểm M là trung điểm của BC.
BB
8 tháng 11 2017
MDA = DAE = AEM = 90
=> ADME là hcn
Tam giác ABC vuông cân tại A
=> ACB = ABC = 45
mà MEC = 90
=> Tam giác EMC vuông cân tại E
=> EM = EC
mà DM = AE (ADME là hcn)
=> EM + DM = EC + AE = AC = 4 (cm)
PADME = 2 . (EM + DM) = 2 . 4 = 8 (cm)
DE = AM (ADME là hcn)
=> DE nhỏ nhất
<=> AM nhỏ nhất
<=> AM _I_ BC tại M
mà tam giác ABC vuông cân tại A
=> AM là đường trung tuyến
=> M là trung điểm
Vậy DE nhỏ nhất <=> M là trung điểm của BC.
14 tháng 8 2023
a)MD vuông góc với AB --> ^MDA=90 độ
ME vuông góc với AC --> ^MEA=90 độ
Mà ^DAE=90 độ => ADME là hình chữ nhật
Tam giác BDM vuông có ^DMB = 45 độ
=> DM=DB
=>Pdme= 2(DM+DA)=2(DB+DA)=2AB=2AC=8(cm)
b) Gọi M' là chân đường cao hạ từ A xuống BC
Ta có: DE=AM ( ADME là hình chữ nhật)
Mà AM≥AM' (Theo tính chất đường xiên)
=> DEmin khi M là chân đường cao hạ từ A xuống BC
PA
21 tháng 10 2016
MDA = DAE = AEM = 90
=> ADME là hcn
Tam giác ABC vuông cân tại A
=> ACB = ABC = 45
mà MEC = 90
=> Tam giác EMC vuông cân tại E
=> EM = EC
mà DM = AE (ADME là hcn)
=> EM + DM = EC + AE = AC = 4 (cm)
PADME = 2 . (EM + DM) = 2 . 4 = 8 (cm)
DE = AM (ADME là hcn)
=> DE nhỏ nhất
<=> AM nhỏ nhất
<=> AM _I_ BC tại M
mà tam giác ABC vuông cân tại A
=> AM là đường trung tuyến
=> M là trung điểm
Vậy DE nhỏ nhất <=> M là trung điểm của BC.
CM
5 tháng 2 2017
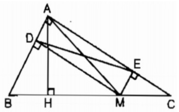
Ta có: AH ⊥ BC nên AM ≥ AH (quan hệ đường vuông góc và đường xiên)
Dấu “=” xảy ra khi M trùng với H
Mà DE = AM ( chứng minh trên)
Vậy DE có độ dài nhỏ nhất bằng AH khi M là chân đường vuông góc kẻ từ A đến BC
17 tháng 9 2021
a: Xét tứ giác ADME có
\(\widehat{EAD}=\widehat{AEM}=\widehat{ADM}=90^0\)
Do đó: ADME là hình chữ nhật
Gọi H là trung điểm của BC
\(\Rightarrow AH\perp BC\)( tính chất tam giác cân )
\(AM\ge AH\)( Dấu "=" xảy ra khi M trùng với H )
Tứ giác ADME là hình chữ nhật ( phần này bạn tự chứng minh )
\(\Rightarrow AM=DE\)( tính chất hình chữ nhật )
\(\Rightarrow DE\ge AH\)
Vậy DE = AH có độ dài nhỏ nhất khi có điểm M là trung điểm của BC
cảm ơn bạn nhiều