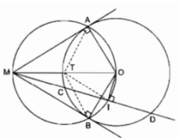
cho đương ton (C) tâm O bán kính và điểm M năm ngoai đương ton đó. Qua M ke hai tiếp tuyến MA, MB tới C. Đương thăng đi qua m khong đi qua tâm O cắt đương tròn (C) tại hai điểm phân biệtbiệt C và D, điểm C nằm giữa hai điểm M va DD. Gọi I la trung điêm của đoạn CD
1) Chứng minh 4 điểm M, A, O, I thuộc 1 đuong tròn
2)Biết MO=3/2R. Tính tích MC.MD theo R





1: ΔOCD cân tại O
mà OI là đường trung tuyến
nên OI\(\perp\)CD
Xét tứ giác OIAM có \(\widehat{OIM}=\widehat{OAM}=90^0\)
nên OIAM là tứ giác nội tiếp
=>O,I,A,M cùng thuộc một đường tròn
2: ΔOAM vuông tại A
=>\(AO^2+AM^2=MO^2\)
=>\(AM^2=\left(\dfrac{3R}{2}\right)^2-R^2=\dfrac{5}{4}R^2\)
Xét (O) có
\(\widehat{MAC}\) là góc tạo bởi tiếp tuyến AM và dây cung AC
\(\widehat{ADC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{MAC}=\widehat{ADC}\)
Xét ΔMAC và ΔMDA có
\(\widehat{MAC}=\widehat{MDA}\)
\(\widehat{AMC}\) chung
Do đó: ΔMAC~ΔMDA
=>\(\dfrac{MA}{MD}=\dfrac{MC}{MA}\)
=>\(MC\cdot MD=MA^2=\dfrac{5}{4}R^2\)