cho a b c là độ dài 3 cạnh tam giác p là nửa chu vi chứng minh ab/(p-c) + bc/(p-a) + ca/(p-b)>=4p
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(S=\frac{ab}{p-c}+\frac{bc}{p-a}+\frac{ca}{p-b}\)
Bất đẳng thức cần chứng minh tương đương với \(S=\frac{2ab}{a+b-c}+\frac{2bc}{b+c-a}+\frac{2ca}{c+a-b}\ge2\left(a+b+c\right)\)
Đặt \(a+b-c=x;b+c-a=y;c+a-b=z\)thì \(x+y+z=a+b+c;a=\frac{y+z}{2};b=\frac{z+x}{x};c=\frac{x+y}{2}\)
Ta cần chứng minh \(S=\text{∑}_{cyc}\frac{\left(y+z\right)\left(z+x\right)}{2z}\ge2\left(x+y+z\right)\)
Ta có:
\(S=\frac{\left(y+z\right)\left(z+x\right)}{2z}+\frac{\left(x+y\right)\left(y+z\right)}{2y}+\frac{\left(z+x\right)\left(x+y\right)}{2x}\)
\(=\frac{xy+yz+zx+z^2}{2z}+\frac{xy+zx+yz+y^2}{2y}+\frac{x^2+xy+zx+yz}{2x}\)
 Đẳng thức xảy ra khi a = b = c
Đẳng thức xảy ra khi a = b = c

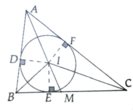
a, Áp dụng tính chất 2 tiếp tuyến tại A,B,C ta chứng minh được b + c - a 2 = AD
b, S A B C = S A I B + S B I C + S C I A
Mà ID = IE = IF = r => S A B C = p.r
c, Vì AM là phân giác của
B
A
C
^
=>
B
M
M
C
=
B
A
A
C
Áp dụng tính chất tỉ lệ thức thu được BM = a c c + b

a,b,c là độ dài 3 cạnh của 1 tam giác nên:
\(\hept{\begin{cases}a< b+c\\b< c+a\\c< a+b\end{cases}}\Leftrightarrow\hept{\begin{cases}a^2< ab+ac\\b^2< bc+ab\\c^2< ac+bc\end{cases}}\)
Cộng từng vế của các BĐT trên:
\(a^2+b^2+c^2< 2\left(ab+bc+ac\right)\)
\(\Rightarrow a^2+b^2+c^2+2\left(ab+bc+ac\right)\)\(< 4\left(ab+bc+ac\right)\)
\(\Rightarrow\left(a+b+c\right)^2\)\(< 4\left(ab+bc+ac\right)\)(đpcm)

Ta có:
a<b+ca<b+c
--> a+a<a+b+ca+a<a+b+c
--> 2a<22a<2
--> a<1a<1
Tương tự ta có : b<1,c<1b<1,c<1
Suy ra: (1−a)(1−b)(1−c)>0(1−a)(1−b)(1−c)>0
⇔ (1–b–a+ab)(1–c)>0(1–b–a+ab)(1–c)>0
⇔ 1–c–b+bc–a+ac+ab–abc>01–c–b+bc–a+ac+ab–abc>0
⇔ 1–(a+b+c)+ab+bc+ca>abc1–(a+b+c)+ab+bc+ca>abc
Nên abc<−1+ab+bc+caabc<−1+ab+bc+ca
⇔ 2abc<−2+2ab+2bc+2ca2abc<−2+2ab+2bc+2ca
⇔ a2+b2+c2+2abc<a2+b2+c2–2+2ab+2bc+2caa2+b2+c2+2abc<a2+b2+c2–2+2ab+2bc+2ca
⇔ a2+b2+c2+2abc<(a+b+c)2−2a2+b2+c2+2abc<(a+b+c)2−2
⇔ a2+b2+c2+2abc<22−2a2+b2+c2+2abc<22−2 , (do a+b=c=2a+b=c=2 )
⇔ dpcm
