bạn nào biết thì giúp mình với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Bạn nào biết thì giúp mình với
11 tháng 3 2022
Ta có \(2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2021}\)
\(\Rightarrow2A-A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2021}-\dfrac{1}{2}-\dfrac{1}{2^2}-...-\dfrac{1}{2^{2022}}=1-\dfrac{1}{2^{2022}}=\dfrac{2^{2022}-1}{2^{2022}}\)
VL
0
31 tháng 8 2021
1: Xét ΔABC có AB=AC
nên ΔABC cân tại A
Suy ra: \(\widehat{ABC}=\widehat{ACB}\)
Xét ΔABH và ΔACH có
AB=AC
AH chung
BH=CH
Do đó: ΔABH=ΔACH
Suy ra: \(\widehat{AHB}=\widehat{AHC}\)
mà \(\widehat{AHB}+\widehat{AHC}=180^0\)
nên \(\widehat{AHB}=\widehat{AHC}=\dfrac{180^0}{2}=90^0\)
Do đó: AH\(\perp\)BC
ND
1
21 tháng 10 2019
Lạc Long Quân, Thánh Gióng, Bánh Chưng Bánh Giày, Sơn Tinh Thủy Tinh, Chử Đồng Tử, Cột Đá Thề, Mai An Tiêm
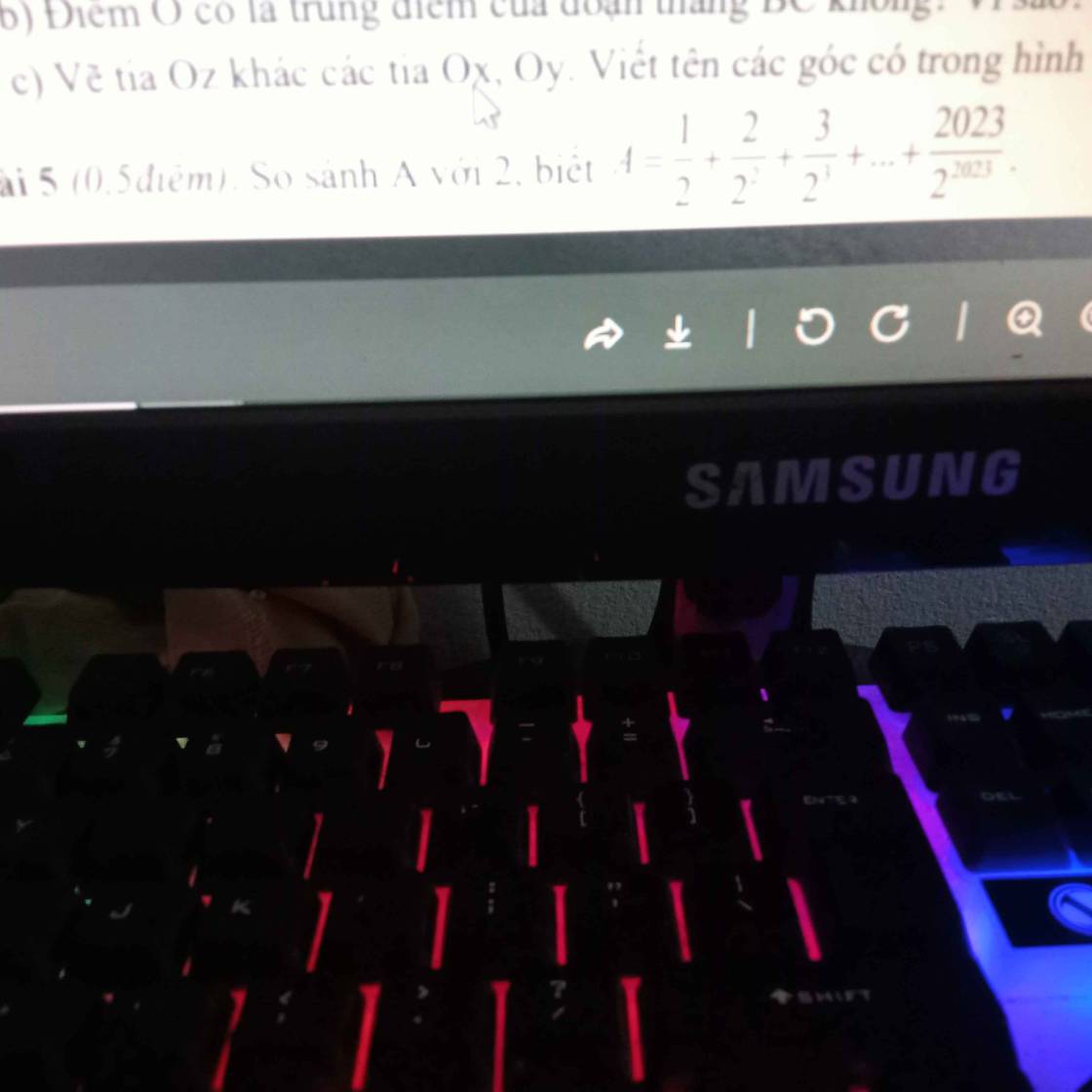
\(A=\dfrac{1}{2^1}+\dfrac{2}{2^2}+\dfrac{3}{2^3}+...+\dfrac{2023}{2^{2023}}\)
\(\Rightarrow2A=1+\dfrac{2}{2^1}+\dfrac{3}{2^2}+...+\dfrac{2023}{2^{2022}}\)
Trừ vế cho vế:
\(\Rightarrow2A-A=1+\dfrac{1}{2^1}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2022}}-\dfrac{2023}{2^{2023}}\)
\(\Rightarrow A=1+\dfrac{1}{2^1}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2022}}-\dfrac{2023}{2^{2023}}\)
\(\Rightarrow2A=2+1+\dfrac{1}{2^1}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2021}}-\dfrac{2023}{2^{2022}}\)
Trừ vế cho vế:
\(2A-A=2-\dfrac{2024}{2^{2022}}+\dfrac{2023}{2^{2023}}\)
\(\Rightarrow A=2-\dfrac{1}{2^{2022}}\left(2024-\dfrac{2023}{2}\right)\)
\(\Rightarrow A=2-\dfrac{2025}{2^{2023}}< 2\)
Vậy \(A< 2\)