1/x^2 + 3x + 2 + 1/x^2 + 5x + 6 + 1/x^2 + 7x + 12 + ... + 1/x^2+25+156 = 3/91
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/ \(\dfrac{1}{x^2+x}+\dfrac{1}{x^2+3x+2}+\dfrac{1}{x^2+5x+6}+\dfrac{1}{x^2+7x+12}\)
\(=\dfrac{1}{x\left(x+1\right)}+\dfrac{1}{\left(x+1\right)\left(x+2\right)}+\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+4\right)}\)
\(=\dfrac{1}{x}-\dfrac{1}{x+1}+\dfrac{1}{x+1}-\dfrac{1}{x+2}+\dfrac{1}{x+2}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+4}\)
\(=\dfrac{1}{x}-\dfrac{1}{x+4}\)
Vậy..
b/ \(\dfrac{1}{x^2+3x+2}+\dfrac{1}{x^2+5x+6}+\dfrac{1}{x^2+7x+12}+\dfrac{1}{x^2+9x+20}\)
\(=\dfrac{1}{\left(x+1\right)\left(x+2\right)}+\dfrac{1}{\left(x+2\right)\left(x+3\right)}+\dfrac{1}{\left(x+3\right)\left(x+4\right)}+\dfrac{1}{\left(x+4\right)\left(x+5\right)}\)
\(=\dfrac{1}{x+1}-\dfrac{1}{x+2}+\dfrac{1}{x+2}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+4}+\dfrac{1}{x+4}-\dfrac{1}{x+5}\)
\(=\dfrac{1}{x+1}-\dfrac{1}{x+5}\)
Vậy..

1) x2 -7x + 10 = x2 - 2x - 5x + 10 = x(x - 2) - 5(x - 2) = (x - 5)(x - 2)
2) x2 + 3x + 2 = x2 + 2x + x + 2 = x(x + 2) + (x + 2) = (x + 1)(x + 2)
3) x2 - 7x + 12 = x2 - 3x - 4x + 12 = x(x - 3) - 4(x - 3) = (x - 3)(x - 4)
4) x2 + 7x + 12 = x2 + 3x + 4x + 12 = x(x + 3) + 4(x + 3) = (x + 3)(x + 4)
5) 16x - 5x2 - 3 = 15x - 5x2 + x - 3 = -5x(x - 3) + (x - 3) = (x - 3)(1 - 5x)
6) 6x2 + 7x - 3 = 6x2 - 2x + 9x - 3 = 2x(3x - 1) + 3(3x - 1) = (2x + 3)(3x - 1)
7) 3x2 - 3x - 6 = 3x2 - 6x + 3x - 6 = 3x(x - 2) + 3(x - 2) = (x - 2)(3x + 3) = 3(x - 2)(x + 1)
8) 3x2 + 3x - 6 = 3x2 - 3x + 6x - 6 = 3x(x - 1) + 6(x - 1) = (x - 1)(3x + 6) = 3(x - 1)(x + 2)
9) 6x2 - 13x + 6 = 6x2 - 9x - 4x + 6 = 3x(2x - 3) - 2(2x - 3) = (3x - 2)(2x - 3)
10) 6x2 + 15x + 6 = 6x2 + 12x + 3x + 6 = 6x(x + 2) + 3(x + 2) = (x + 2)(6x + 3) = 3(x + 2)(3x + 1)
11) 6x2 - 20x + 6 = 6x2 - 18x - 2x + 6 = 6x(x -3) - 2(x - 3) = (6x - 2)(x - 3) = 2(3x - 1)(x - 3)
12) 8x2 + 5x - 3 = 8x2 + 8x - 3x - 3 = 8x(x + 1) - 3(x + 1) = (x + 1)(8x - 3)

x2-4x+7 = 0 ⇔ x2 -4x + 4 + 3 = 0
⇔ (x-2)2+3=0 ⇔ (x-2)2=-3 (vô lí)
Vậy pt vô nghiệm
*Chứng minh phương trình \(x^2-4x+7=0\) vô nghiệm
Ta có: \(x^2-4x+7=0\)
\(\Leftrightarrow x^2-4x+4+3=0\)
\(\Leftrightarrow\left(x-2\right)^2+3=0\)
mà \(\left(x-2\right)^2+3\ge3>0\forall x\)
nên \(x\in\varnothing\)(đpcm)

a) \(5x\left(\frac{1}{5}x-2\right)+3\left(6-\frac{1}{3}x^2\right)=12\)
=> \(x^2-10x+18-x^2=12\)
=> -10x + 18 = 12
=> -10x = -6
=> -5x = -3
=> x = 3/5
b) 7x(x - 2) - 5(x - 1) = 7x2 + 3
=> 7x2 - 14x - 5x + 5 = 7x2 + 3
=> 7x2 - 14x - 5x + 5 - 7x2 - 3 = 0
=> -19x + 2 = 0
=> -19x = -2
=> x = \(\frac{2}{19}\)
c) 2(5x - 8) - 3(4x - 5) = 4(3x - 4) + 11
=> 10x - 16 - 12x + 15 = 12x - 16 + 11
=> 10x - 16 - 12x + 15 - 12x + 16 - 11 = 0
=> (10x - 12x - 12x) + (-16 + 15 + 16 - 11) = 0
=> -14x + 4 = 0
=> -14x = -4
=> -7x = -2
=> x = 2/7

Bài 2:
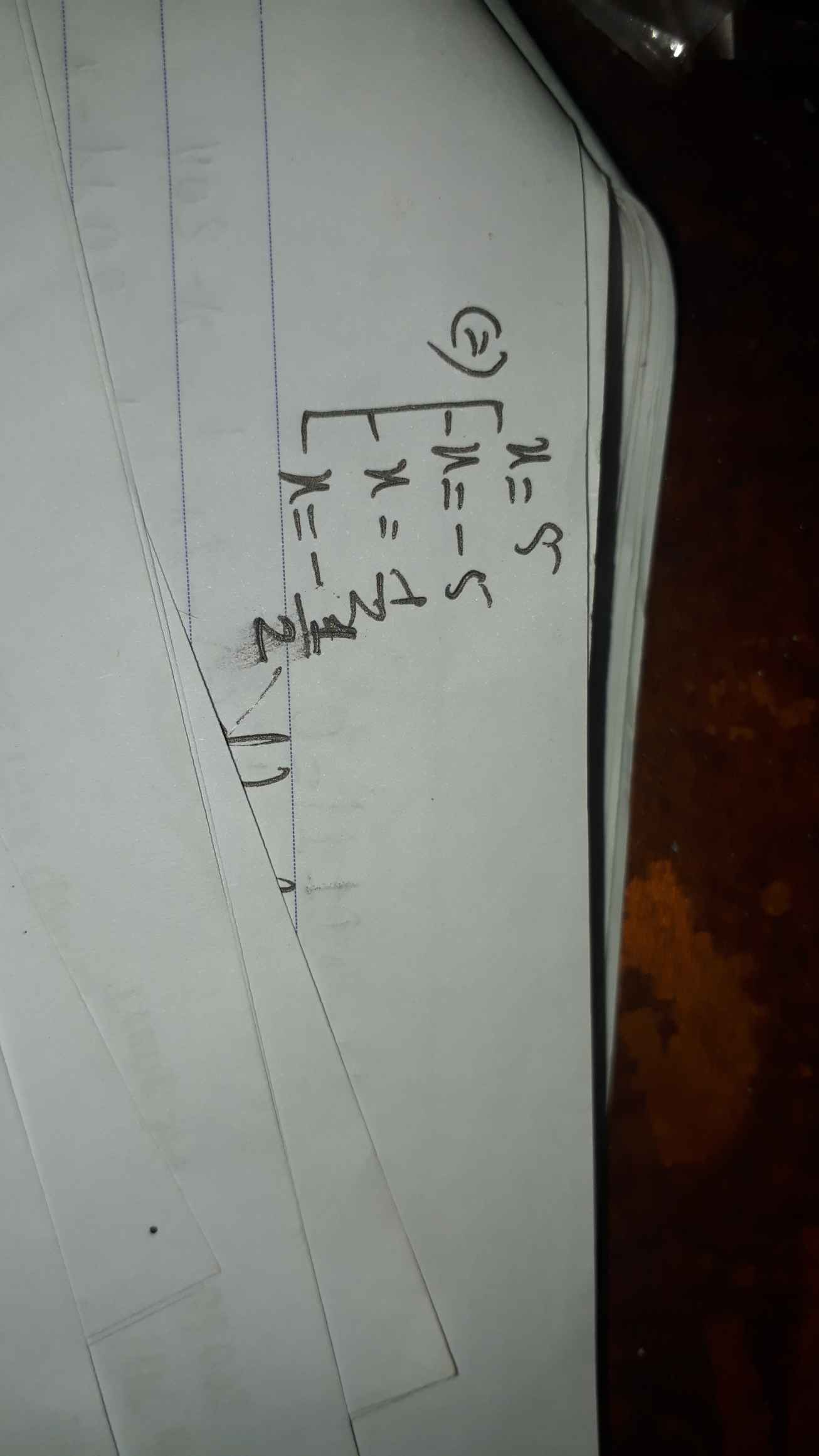
a: \(\Leftrightarrow\left(x-2\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)

\(\Leftrightarrow\dfrac{1}{x+1}-\dfrac{1}{x+2}+\dfrac{1}{x+2}-\dfrac{1}{x+3}+\dfrac{1}{x+3}-\dfrac{1}{x+4}=\dfrac{3}{10}\)
\(\Leftrightarrow\dfrac{x+4-x-1}{\left(x+4\right)\left(x+1\right)}=\dfrac{3}{10}\)
\(\Leftrightarrow\left(x+4\right)\left(x+1\right)=10\)
\(\Leftrightarrow x^2+5x-6=0\)
=>(x+6)(x-1)=0
=>x=-6 hoặc x=1

=>\(\dfrac{-1}{x-1}+\dfrac{1}{x-2}-\dfrac{1}{x-2}+\dfrac{1}{x-3}-\dfrac{1}{x-3}+\dfrac{1}{x-4}=2\)
=>\(\dfrac{1}{x-4}-\dfrac{1}{x-1}=2\)
=>\(\dfrac{x-1-x+4}{x^2-5x+4}=2\)
=>2x^2-10x+8=3
=>2x^2-10x+5=0
=>\(x=\dfrac{5\pm\sqrt{15}}{2}\)

 Bài 1.
Bài 1.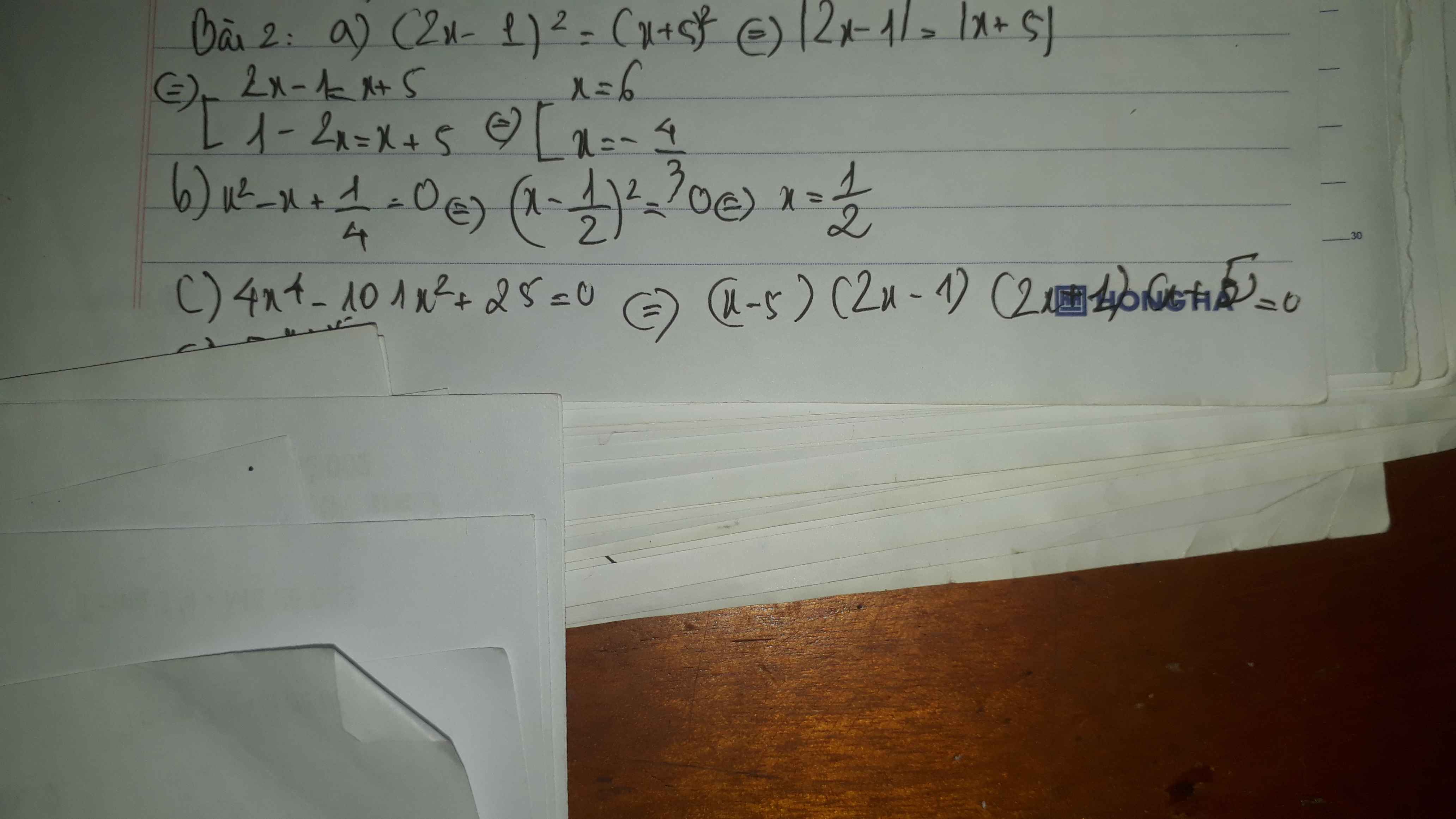
ĐKXĐ: \(x\notin\left\{-1;-2;...;-13\right\}\)
\(\dfrac{1}{x^2+3x+2}+\dfrac{1}{x^2+5x+6}+...+\dfrac{1}{x^2+25x+156}=\dfrac{3}{91}\)
=>\(\dfrac{1}{\left(x+1\right)\left(x+2\right)}+\dfrac{1}{\left(x+2\right)\left(x+3\right)}+...+\dfrac{1}{\left(x+12\right)\left(x+13\right)}=\dfrac{3}{91}\)
=>\(\dfrac{1}{x+1}-\dfrac{1}{x+2}+\dfrac{1}{x+2}-\dfrac{1}{x+3}+...+\dfrac{1}{x+12}-\dfrac{1}{x+13}=\dfrac{3}{91}\)
=>\(\dfrac{1}{x+1}-\dfrac{1}{x+13}=\dfrac{3}{91}\)
=>\(\dfrac{12}{\left(x+1\right)\left(x+13\right)}=\dfrac{3}{91}\)
=>\(\dfrac{4}{\left(x+1\right)\left(x+13\right)}=\dfrac{1}{91}\)
=>(x+1)(x+13)=364
=>\(x^2+14x+13-364=0\)
=>\(x^2+14x-351=0\)
=>(x+27)(x-13)=0
=>\(\left[{}\begin{matrix}x=13\left(nhận\right)\\x=-27\left(nhận\right)\end{matrix}\right.\)