Cho tam giác ABC nhọn ,các đường cao BD và CE cắt nhau tại H .Đường vuông góc với AB tại B và đường vg góc vs AC tại C cắt nhau tại K .Gọi M là trung điểm củaBC .Cmr:
a) ∆ADB ~ ∆AEC và ∆AED ~ ∆ACB
b) HE.HC = HD.HB
c) H ,M ,K thẳng hàng và góc AED = góc ACB
d)AH cắt BC tại O. Cm: BE.BA + CD.CA = BC^2
e) HO/AO + HD/BD + HE/CE = 1
f) H là giao điểm các đường phân giác của ∆ODE
g) Cho góc ACB=45° . Gọi P là trung điểm của DC...
Đọc tiếp
Cho tam giác ABC nhọn ,các đường cao BD và CE cắt nhau tại H .Đường vuông góc với AB tại B và đường vg góc vs AC tại C cắt nhau tại K .Gọi M là trung điểm củaBC .Cmr:
a) ∆ADB ~ ∆AEC và ∆AED ~ ∆ACB
b) HE.HC = HD.HB
c) H ,M ,K thẳng hàng và góc AED = góc ACB
d)AH cắt BC tại O. Cm: BE.BA + CD.CA = BC^2
e) HO/AO + HD/BD + HE/CE = 1
f) H là giao điểm các đường phân giác của ∆ODE
g) Cho góc ACB=45° . Gọi P là trung điểm của DC .Từ D kẻ đường thẳng vg góc vs BP tại I và cắt CK tại N . Tìm tỉ số diện tích của tứ giác CPIN và diện tích ∆DCN.
GIÚP MK VS Ạ ,MK ĐAG CẦN GẤP LẮM Ạ
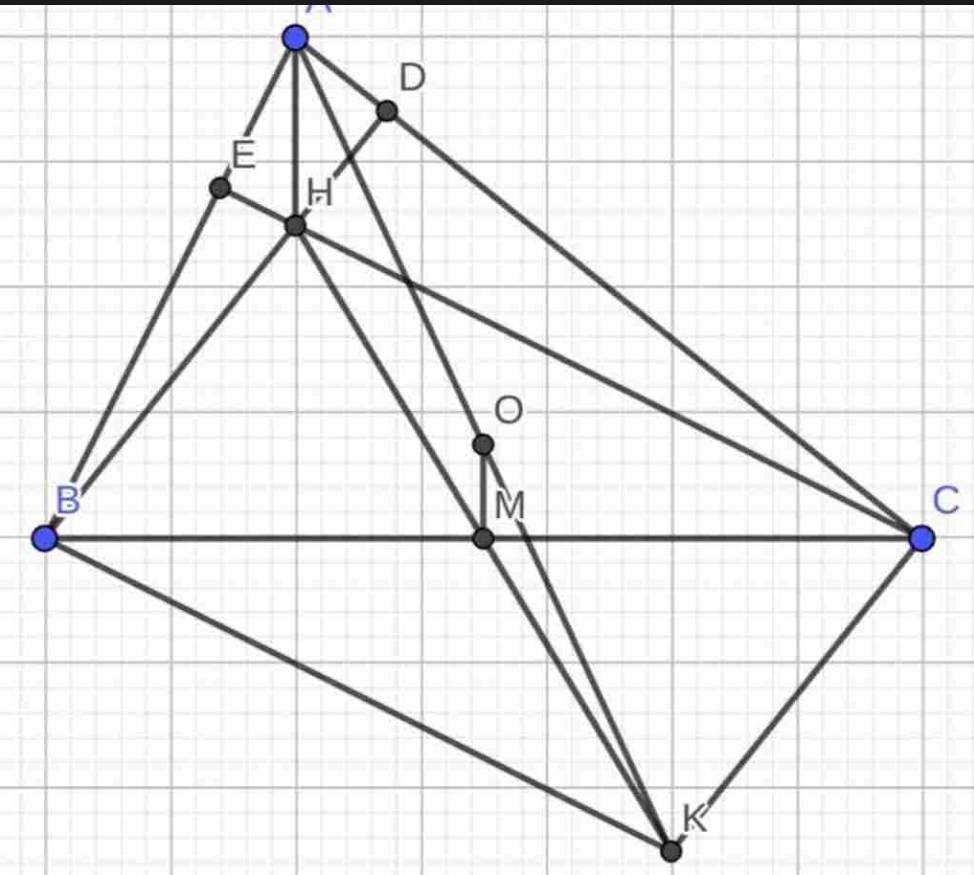
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{DAB}\) chung
Do đó: ΔADB~ΔAEC
=>\(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
=>\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét ΔADE và ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
\(\widehat{DAE}\) chung
Do đó: ΔADE~ΔABC
=>\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét ΔADE và ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
\(\widehat{DAE}\) chung
Do đó: ΔADE~ΔABC
b: Xét ΔHEB vuông tại E và ΔHDC vuông tại D có
\(\widehat{EHB}=\widehat{DHC}\)(hai góc đối đỉnh)
Do đó: ΔHEB~ΔHDC
=>\(\dfrac{HE}{HD}=\dfrac{HB}{HC}\)
=>\(HE\cdot HC=HB\cdot HD\)
c: Ta có: BH\(\perp\)AC tại D
CK\(\perp\)AC
Do đó: BH//CK
ta có:CH\(\perp\)AB
BK\(\perp\)AB
Do đó: CH//BK
Xét tứ giác BHCK có
BH//CK
BK//CH
Do đó: BHCK là hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HK
=>H,M,K thẳng hàng
ΔAED~ΔACB
=>\(\widehat{AED}=\widehat{ACB}\)
d: Xét ΔABC có
BD,CE là các đường cao
BD cắt CE tại H
Do đó: H là trực tâm của ΔABC
=>AH\(\perp\)BC tại O
Xét ΔBEC vuông tại Evà ΔBOA vuông tại O có
\(\widehat{EBC}\) chung
Do đó:ΔBEC~ΔBOA
=>\(\dfrac{BE}{BO}=\dfrac{BC}{BA}\)
=>\(BE\cdot BA=BO\cdot BC\)
Xét ΔCDB vuông tại D và ΔCOA vuông tại O có
\(\widehat{DCB}\) chung
DO đó: ΔCDB~ΔCOA
=>\(\dfrac{CD}{CO}=\dfrac{CB}{CA}\)
=>\(CD\cdot CA=CO\cdot CB\)
\(BE\cdot BA+CD\cdot CA\)
\(=BO\cdot BC+CO\cdot BC\)
\(=BC\left(BO+CO\right)=BC^2\)
Phần e,f,g đou ạ