P(x)= x^2023 - 2022x^2022 - 2022x^2021 - ... - 2022x^2 - 2022x + 1
Tính P(2023)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
HM
1
Những câu hỏi liên quan
NB
1
TD
1
DD
Đoàn Đức Hà
Giáo viên
9 tháng 6 2021
\(Q\left(x\right)=x^{101}-2020x^{100}-2022x^{99}+2022x^{98}+x-2021\)
\(=x^{100}\left(x-2021\right)+x^{99}\left(x-2021\right)-x^{98}\left(x-2021\right)+x^{98}+x-2021\)
\(Q\left(2021\right)=0+0-0+2021^{98}+0=2021^{98}\)
TD
1
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
Các đa thức một biến là: a,b,d.
a) \( - 7x + 5\): biến của đa thức là x và bậc của đa thức là 1.
b) \(2021{x^2} - 2022x + 2023\): biến của đa thức là x và bậc của đa thức là 2
d) \( - 2{t^m} + 8{t^2} + t - 1\), với m là số tự nhiên lớn hơn 2: biến của đa thức là t và bậc của đa thức là m.
PA
1
TA
22 tháng 7 2021
Thay `x=2021` vào A: `A=2020.2021-2022 .2021^2 +2021^3=-2021`
NC
1
NG
1
20 tháng 10 2023
a: \(2022^{x-2021}+3=\left(7-5\right)^2\)
=>\(2022^{x-2021}+3=4\)
=>\(2022^{x-2021}=1\)
=>x-2021=0
=>x=2021
b: \(\left(x+1\right)+\left(x+2\right)+...+\left(x+30\right)=795\)
=>\(30x+\left(1+2+3+...+30\right)=795\)
=>\(30x+\dfrac{30\cdot31}{2}=795\)
=>\(30x=795-31\cdot15=330\)
=>x=11
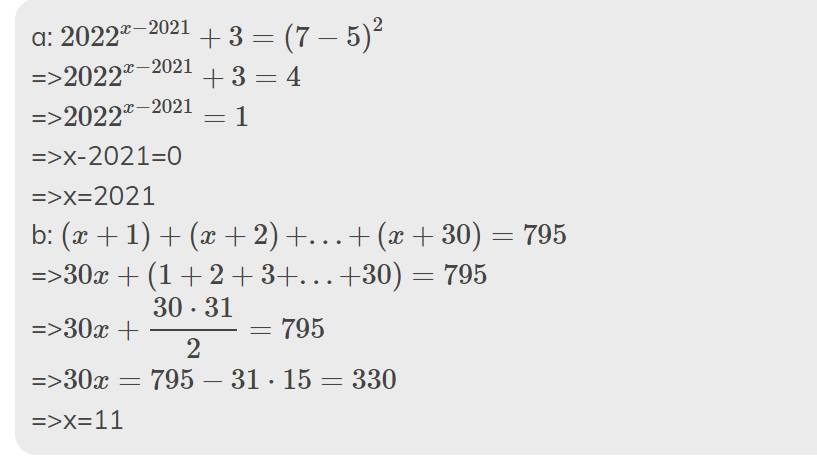
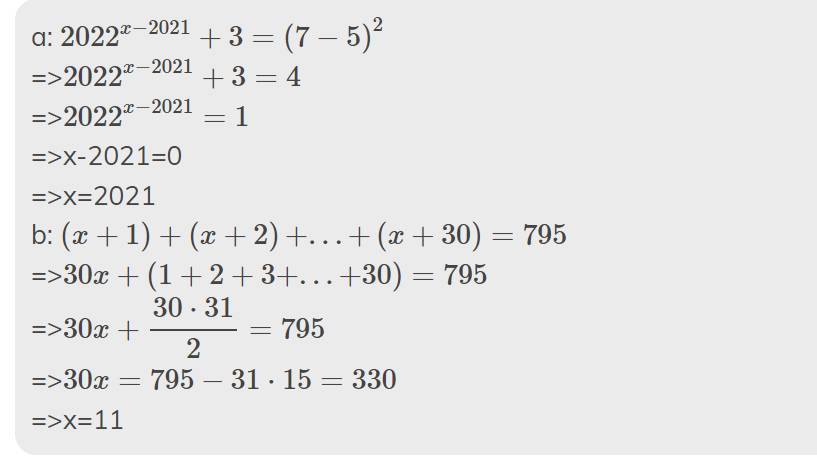
x=2023 nên x-1=2022
\(P=x^{2023}-2022x^{2022}-2021x^{2021}-...-2022x+1\)
\(=x^{2023}-x^{2022}\left(x-1\right)-x^{2021}\left(x-1\right)-...-x\left(x-1\right)+1\)
\(=x^{2023}-x^{2023}+x^{2022}-x^{2022}+...-x^2+x+1\)
=x+1
=2023+1=2024