348 519 x 18
helpppppppppp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: x-4/5=3/7
=>x=3/7+4/5=43/35
b: x+3/7=4/5
=>x=4/5-3/7=13/35
c: 19/20-x=8/5-3/4
=>19/20-x=32/20-15/20=17/20
=>x=2/20=1/10
d: =>4/5*x=2/21
=>x=2/21:4/5=5/42
e: =>x:7/9=6/8
=>x=6/8*7/9=3/4*7/9=21/36=7/12
f: =>x/6=2/3-1/3=1/3
=>x=2

a: x-4/5=3/7
=>x=3/7+4/5=43/35
b: x+3/7=4/5
=>x=4/5-3/7=13/35
c: 19/20-x=8/5-3/4
=>19/20-x=32/20-15/20=17/20
=>x=2/20=1/10
d: =>4/5*x=11/21
=>x=55/84
e: =>x=6/8*7/9=42/72=7/12
f: =>x/6=2/3-1/3=1/3
=>x=2

Tổng của số bị chia, số chia là:
`103,9-0,2-18=85,7`
Số chia là:
`(85,7-0,2):(18+1)xx1=4,5`
Số bị chia là:
`4,5xx18=81`

a: \(=\left(5^2+3\right):7=4\)
b: \(=7^2-3^2+8\cdot25=40+200=240\)




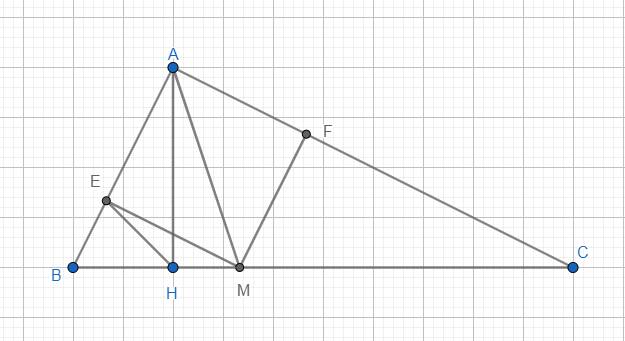
a) Xét △BEM và △BHA có:
\(\hat{B}\): chung
\(\hat{BEM}=\hat{BHA}\) = 90o
Do đó: △BEM đồng dạng △BHA (gg)
=> \(\dfrac{BE}{BH}=\dfrac{BM}{BA}\) => BE.BA = BH.BM
b) Theo câu a), ta có:
BE.BA = BH.BM
=> \(\dfrac{BE}{BM}=\dfrac{BH}{BA}\)
Lại có: \(\hat{B}\): chung
nên △BEH đồng dạng △BMA (cgc)
=> \(\hat{BHE}=\hat{BAM}\)
Vì AM là tia phân giác của \(\hat{BAC}\) nên \(\hat{BAM}=\dfrac{\hat{BAC}}{2}=\dfrac{90^o}{2}=45^0\)
=> \(\hat{BHE}=45^0\)
mà \(\hat{BHA}=90^o\)
Nên HE là tia phân giác góc AHB.
=6273342
6273342