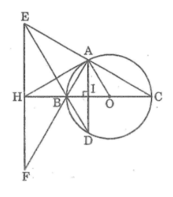
Cho tam giác ABC (AC > AB) nội tiếp đường tròn (O, R) có đường kính BC, về dây
AD vuông góc với BC tại H ( H nằm giữa O và B). Lấy E là điểm chính giữa của cung nhỏ AC. Qua A kẻ đường thẳng vuông góc với tia CE tại K
a. Cho ACB=30°, tính theo R độ dài cung tròn và diện tích hình quạt tròn ứng với cung nhỏ AB. b. Chứng minh AHCK là tứ giác nội tiếp
c. Chứng minh KH// ED
d. Gọi M là giao điểm của ED và BC. Chứng minh EAB = CMD


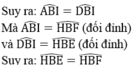
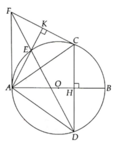
a: Xét (O) có
ΔABC nội tiếp
BC là đường kính
Do đó: ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}+30^0=90^0\)
=>\(\widehat{ABC}=60^0\)
Xét (O) có
\(\widehat{ACB}\)là góc nội tiếp chắn cung AB
nên \(\widehat{AOB}=2\cdot\widehat{ACB}=60^0\)
Độ dài cung tròn AB là:
\(l=\dfrac{\Omega\cdot R\cdot60}{180}=\Omega\cdot\dfrac{R}{3}\)
Diện tích hình quạt tròn ứng với cung AB là:
\(S_{q\left(AB\right)}=\dfrac{\Omega\cdot R^2\cdot60}{360}=\dfrac{\Omega\cdot R^2}{6}\)
b: Xét tứ giác AHCK có \(\widehat{AHC}+\widehat{AKC}=90^0+90^0=180^0\)
nên AHCK là tứ giác nội tiếp
c: Ta có:AHCK là tứ giác nội tiếp
=>\(\widehat{AHK}=\widehat{ACK}=\widehat{ACE}\)
Xét (O) có
\(\widehat{ADE}\) là góc nội tiếp chắn cung AE
\(\widehat{ACE}\) là góc nội tiếp chắn cung AE
Do đó: \(\widehat{ADE}=\widehat{ACE}\)
=>\(\widehat{AHK}=\widehat{ADE}\)
=>HK//DE