 Hộ bài 4 với ạ
Hộ bài 4 với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
\(P=\dfrac{5}{x^2+y^2}+\dfrac{3}{xy}=5\left(\dfrac{1}{x^2+y^2}+\dfrac{1}{2xy}\right)+\dfrac{1}{2xy}\)
Áp dụng bất đẳng thức Bunhiacopxki dạng phân thức ta có:
\(\dfrac{1}{x^2+y^2}+\dfrac{1}{2xy}\ge\dfrac{4}{x^2+2xy+y^2}=\dfrac{4}{\left(x+y\right)^2}=\dfrac{4}{3^2}=\dfrac{4}{9}\)
Áp dụng bất đẳng thức Cosi ta có:
\(a+b\ge2\sqrt{ab}\Rightarrow2ab\le\dfrac{\left(a+b\right)^2}{2}=\dfrac{3^2}{2}=\dfrac{9}{2}\Rightarrow\dfrac{1}{2ab}\ge\dfrac{2}{9}\)
\(\Rightarrow P\ge5\cdot\dfrac{4}{9}+\dfrac{2}{9}=\dfrac{22}{9}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=\dfrac{3}{2}\)

4:
\(A=7^{4n}-1\)
\(=\left(7^4\right)^n-1\)
\(=\left(7^4-1\right)\cdot\left(7^{4\left(n-1\right)}+7^{4\left(n-2\right)}+...+1\right)\)
\(=\left(7^2-1\right)\left(7^2+1\right)\left(7^{4n-4}+7^{4n-8}+...+1\right)\)
\(=50\cdot48\cdot\left(7^{4n-4}+7^{4n-8}+...+1\right)⋮5\)

Y chứa NaOH, NaAlO2
Gọi số mol NaOH, NaAlO2 trong mỗi phần là x, y (mol)
TN1:
\(n_{HCl}=0,1.1=0,1\left(mol\right)\)
PTHH: NaOH + HCl --> NaCl + H2O
0,1<----0,1
=> x = 0,1 (mol)
TN3: nHCl = 0,75.1 = 0,75 (mol)
PTHH: NaOH + HCl --> NaCl + H2O
0,1--->0,1
NaAlO2 + HCl + H2O --> NaCl + Al(OH)3
y------>y------------------------>y
Al(OH)3 + 3HCl --> AlCl3 + 3H2O
\(\dfrac{0,65-y}{3}\)<-(0,65-y)
=> \(n_{Al\left(OH\right)_3\left(3\right)}=y-\dfrac{0,65-y}{3}=\dfrac{4y-0,65}{3}\left(mol\right)\)
TN2: \(n_{HCl}=1.0,45=0,45\left(mol\right)\)
- Nếu kết tủa không bị hòa tan:
PTHH: NaOH + HCl --> NaCl + H2O
0,1--->0,1
NaAlO2 + HCl + H2O --> NaCl + Al(OH)3
0,35<--0,35-------------------->0,35
Điều kiện: y \(\ge\) 0,35
=> \(n_{Al\left(OH\right)_3\left(2\right)}=0,35\left(mol\right)\)
Do \(n_{Al\left(OH\right)_3\left(2\right)}=3.n_{Al\left(OH\right)_3\left(3\right)}\)
=> \(0,35=4y-0,65\)
=> y = 0,25 (Loại)
=> Kết tủa bị hòa tan 1 phần
PTHH: NaOH + HCl --> NaCl + H2O
0,1--->0,1
NaAlO2 + HCl + H2O --> NaCl + Al(OH)3
y---->y------------------------->y
Al(OH)3 + 3HCl --> AlCl3 + 3H2O
\(\dfrac{0,35-y}{3}\)<--(0,35-y)
=> \(n_{Al\left(OH\right)_3\left(2\right)}=y-\dfrac{0,35-y}{3}=\dfrac{4y-0,35}{3}\left(mol\right)\)
Do \(n_{Al\left(OH\right)_3\left(2\right)}=3.n_{Al\left(OH\right)_3\left(3\right)}\)
=> \(\dfrac{4y-0,35}{3}=4y-0,65\)
=> y = 0,2
Vậy trong Y chứa \(\left\{{}\begin{matrix}NaOH:0,3\left(mol\right)\\NaAlO_2:0,6\left(mol\right)\end{matrix}\right.\)
Bảo toàn Na: nNa = 0,9 (mol)
Bảo toàn Al: nAl = 0,6 (mol)
=> m = 0,9.23 + 0,6.27 = 36,9 (g)
Y chứa NaOH, NaAlO2
Gọi số mol NaOH, NaAlO2 trong mỗi phần là x, y (mol)
TN1:
nHCl=0,1.1=0,1(mol)nHCl=0,1.1=0,1(mol)
PTHH: NaOH + HCl --> NaCl + H2O
0,1<----0,1
=> x = 0,1 (mol)
TN3: nHCl = 0,75.1 = 0,75 (mol)
PTHH: NaOH + HCl --> NaCl + H2O
0,1--->0,1
NaAlO2 + HCl + H2O --> NaCl + Al(OH)3
y------>y------------------------>y
Al(OH)3 + 3HCl --> AlCl3 + 3H2O
0,65−y30,65−y3<-(0,65-y)
=> nAl(OH)3(3)=y−0,65−y3=4y−0,653(mol)nAl(OH)3(3)=y−0,65−y3=4y−0,653(mol)
TN2: nHCl=1.0,45=0,45(mol)nHCl=1.0,45=0,45(mol)
- Nếu kết tủa không bị hòa tan:
PTHH: NaOH + HCl --> NaCl + H2O
0,1--->0,1
NaAlO2 + HCl + H2O --> NaCl + Al(OH)3
0,35<--0,35-------------------->0,35
Điều kiện: y ≥≥ 0,35
=> nAl(OH)3(2)=0,35(mol)nAl(OH)3(2)=0,35(mol)
Do nAl(OH)3(2)=3.nAl(OH)3(3)nAl(OH)3(2)=3.nAl(OH)3(3)
=> 0,35=4y−0,650,35=4y−0,65
=> y = 0,25 (Loại)
=> Kết tủa bị hòa tan 1 phần
PTHH: NaOH + HCl --> NaCl + H2O
0,1--->0,1
NaAlO2 + HCl + H2O --> NaCl + Al(OH)3
y---->y------------------------->y
Al(OH)3 + 3HCl --> AlCl3 + 3H2O
0,35−y30,35−y3<--(0,35-y)
=> nAl(OH)3(2)=y−0,35−y3=4y−0,353(mol)nAl(OH)3(2)=y−0,35−y3=4y−0,353(mol)
Do nAl(OH)3(2)=3.nAl(OH)3(3)nAl(OH)3(2)=3.nAl(OH)3(3)
=> 4y−0,353=4y−0,654y−0,353=4y−0,65
=> y = 0,2
Vậy trong Y chứa {NaOH:0,3(mol)NaAlO2:0,6(mol){NaOH:0,3(mol)NaAlO2:0,6(mol)
Bảo toàn Na: nNa = 0,9 (mol)
Bảo toàn Al: nAl = 0,6 (mol)
=> m = 0,9.23 + 0,6.27 = 36,9 (g)

Câu 3:
Gọi độ dài quãng đường AB là x(km)
Thời gian xe máy đi từ A đến B là: \(\dfrac{x}{30}\left(h\right)\)
Thời gian xe máy đi từ B về A là: \(\dfrac{x}{35}\left(h\right)\)
Theo đề, ta có phương trình: \(\dfrac{x}{30}+\dfrac{x}{35}=\dfrac{13}{3}\)
\(\Leftrightarrow\dfrac{7x}{210}+\dfrac{6x}{210}=\dfrac{910}{210}\)
\(\Leftrightarrow13x=910\)
hay x=70(thỏa ĐK)
Vậy: Độ dài quãng đường AB là 70km

1: Xét (O) có
DC là tiếp tuyến
DA là tiếp tuyến
Do đó: DC=DA
Xét (O) có
EC là tiếp tuyến
EB là tiếp tuyến
Do đó: EC=EB
Ta có: DC+EC=DE
nên DE=AC+EB



Bài 3:
1: Ta có: \(P=\dfrac{\sqrt{x}+1}{\sqrt{x}-2}+\dfrac{2\sqrt{x}}{\sqrt{x}+2}-\dfrac{5\sqrt{x}+2}{x-4}\)
\(=\dfrac{x+3\sqrt{x}+2+2x-4\sqrt{x}-5\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}+2}\)

Câu 1: Vì (d') vuông góc với (d) nên \(a\cdot\dfrac{-1}{3}=-1\)
hay a=3
Vậy: (d'): y=3x+b
Thay x=4 và y=-5 vào (d'), ta được:
b+12=-5
hay b=-17


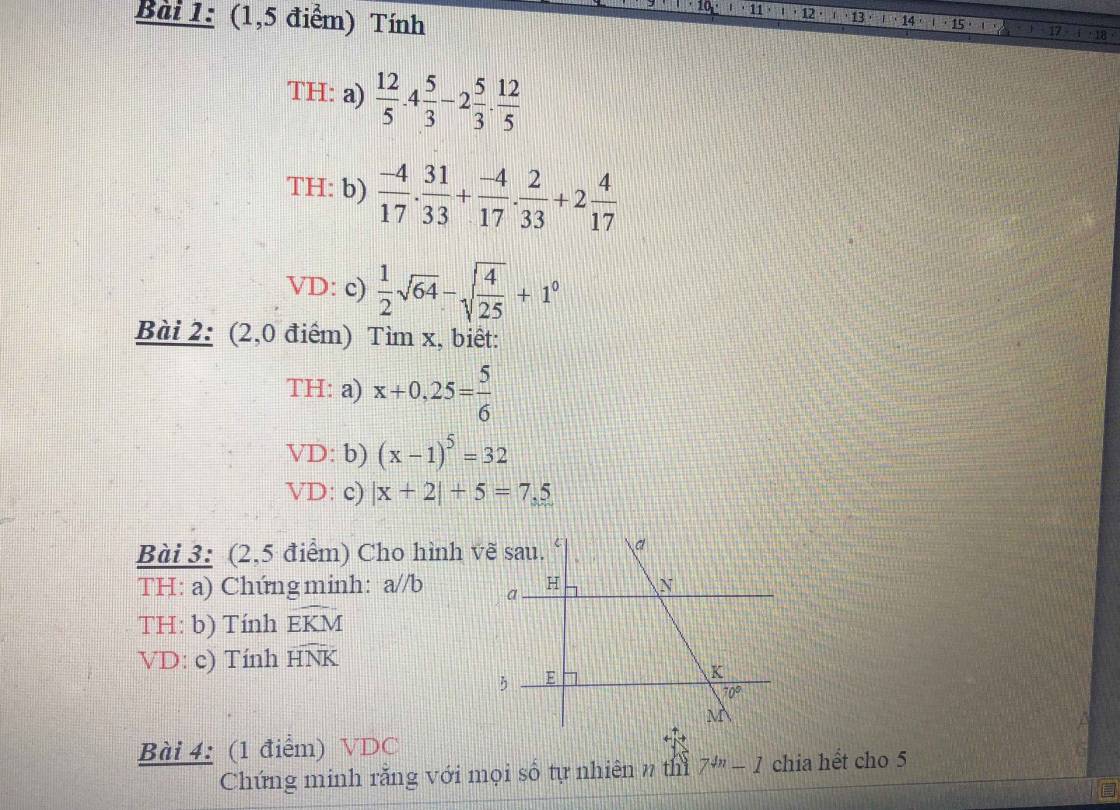 giải hộ mình bài 4 với ạ
giải hộ mình bài 4 với ạ 



 lm hộ em bài 3 4 5 6 với ạ e cảm ơn
lm hộ em bài 3 4 5 6 với ạ e cảm ơn

a) Do I là trung điểm của BC (gt)
⇒ BI = CI
Do ∆ABC cân tại A (gt)
⇒ AB = AC
Xét ∆AIB và ∆AIC có:
AB = AC (cmt)
AI là cạnh chung
BI = CI (cmt)
⇒ ∆AIB = ∆AIC (c-c-c)
b) Do AB = AC (cmt)
⇒ A nằm trên đường trung trực của BC (1)
Do BI = CI (cmt)
⇒ I nằm trên đường trung trực của BC (2)
Từ (1) và (2) ⇒ AI là đường trung trực của BC
⇒ AI ⊥ BC
c) ∆ABC cân tại A (gt)
AI là đường trung trực của BC
⇒ AI là đường phân giác của ∆ABC
⇒ ∠BAI = ∠CAI
⇒ ∠MAI = ∠NAI
Xét hai tam giác vuông: ∆AIM và ∆AIN có:
AI là cạnh chung
∠MAI = ∠NAI (cmt)
⇒ ∆AIM = ∆AIN (cạnh huyền - góc nhọn)
⇒ IM = IN (hai cạnh tương ứng)
⇒ ∆IMN cân tại I