Tìm a và b thỏa mãn ab = ba với ĐK a ≠ b.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
L
3
18 tháng 1 2017
\(GTLN=\frac{2005^2}{4}\) Khi \(\hept{\begin{cases}a=\frac{2005}{2}\\b=\frac{2005}{2}\end{cases}}\)
PT
1
CM
16 tháng 11 2017
Thế b=9a vào đẳng thức còn lại ta được
a 9 a = ( 9 a ) a ⇒ ( a 9 ) a ⇒ a 9 = 9 a ⇒ a 8 = 9 ( do a > 0)
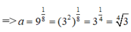
Chọn đáp án B
TX
1
12 tháng 4 2018
\(Từ GT, ta có: \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}\ge6\) Áp dụng bđt AM - GM, ta lại có: \(\frac{1}{a^2}+1\ge\frac{2}{a};\frac{1}{b^2}+1\ge\frac{2}{b};\frac{1}{c^2}+1\ge\frac{2}{c}\) \(\frac{1}{a^2}+\frac{1}{b^2}\ge\frac{2}{ab};\frac{1}{b^2}+\frac{1}{c^2}\ge\frac{2}{bc};\frac{1}{c^2}+\frac{1}{a^2}\ge\frac{2}{ac}\) Cộng theo vế ta có: \(3\left(\text{∑}\frac{1}{a^2}\right)+3\ge2\left(\text{∑}\frac{1}{a}+\text{∑}\frac{1}{ab}\right)\Leftrightarrow\text{∑}\frac{1} {a^2}\ge3\left(đ\text{pcm}\right)\) \(\text{Dau }"="\Leftrightarrow a=b=c=1\)
11 tháng 4 2018
Từ GT, ta có: \(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}+\frac{1}{ab}+\frac{1}{bc}+\frac{1}{ca}\ge6\)
Áp dụng bđt AM - GM, ta lại có:
\(\frac{1}{a^2}+1\ge\frac{2}{a};\frac{1}{b^2}+1\ge\frac{2}{b};\frac{1}{c^2}+1\ge\frac{2}{c}\)
\(\frac{1}{a^2}+\frac{1}{b^2}\ge\frac{2}{ab};\frac{1}{b^2}+\frac{1}{c^2}\ge\frac{2}{bc};\frac{1}{c^2}+\frac{1}{a^2}\ge\frac{2}{ac}\)
Cộng theo vế ta có:
\(3\left(\text{∑}\frac{1}{a^2}\right)+3\ge2\left(\text{∑}\frac{1}{a}+\text{∑}\frac{1}{ab}\right)\Leftrightarrow\text{∑}\frac{1}{a^2}\ge3\left(đ\text{pcm}\right)\)
\(\text{Dau }"="\Leftrightarrow a=b=c=1\)
AK
Chờ a , b,c là ba số khác 0 thỏa mãn đk :\(\frac{a+b-c}{c}\)=\(\frac{b+c-a}{a}\)=\(\frac{c+a-b}{b}\)
1
1 tháng 3 2018
Ta có: (a+b-c)/c=(b+c-a)/a=(c+a-b)/b=(a+b-c+b+c... (a+b+c)=(a+b+c)/(a+b+c)=1
=>(a+b-c)/c=1 => a+b-c=c =>a+b=2c (1)
Tương tự: (b+c-a)/a=1 =>b+c=2a (2)
(c+a-b)/b=1 =>c+a=2b (3)
Thay (1), (2), (3) vào P, ta có:
P=(a+b)/a . (b+c)/b .(a+c)/c=2c/a.2a/b.2b/c=2.2.2=8
23 tháng 1 2021
1) Áp dụng bất đẳng thức AM - GM và bất đẳng thức Schwarz:
\(P=\dfrac{1}{a}+\dfrac{1}{\sqrt{ab}}\ge\dfrac{1}{a}+\dfrac{1}{\dfrac{a+b}{2}}\ge\dfrac{4}{a+\dfrac{a+b}{2}}=\dfrac{8}{3a+b}\ge8\).
Đẳng thức xảy ra khi a = b = \(\dfrac{1}{4}\).
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 1 2021
2.
\(4=a^2+b^2\ge\dfrac{1}{2}\left(a+b\right)^2\Rightarrow a+b\le2\sqrt{2}\)
Đồng thời \(\left(a+b\right)^2\ge a^2+b^2\Rightarrow a+b\ge2\)
\(M\le\dfrac{\left(a+b\right)^2}{4\left(a+b+2\right)}=\dfrac{x^2}{4\left(x+2\right)}\) (với \(x=a+b\Rightarrow2\le x\le2\sqrt{2}\) )
\(M\le\dfrac{x^2}{4\left(x+2\right)}-\sqrt{2}+1+\sqrt{2}-1\)
\(M\le\dfrac{\left(2\sqrt{2}-x\right)\left(x+4-2\sqrt{2}\right)}{4\left(x+2\right)}+\sqrt{2}-1\le\sqrt{2}-1\)
Dấu "=" xảy ra khi \(x=2\sqrt{2}\) hay \(a=b=\sqrt{2}\)
3. Chia 2 vế giả thiết cho \(x^2y^2\)
\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{x^2}+\dfrac{1}{y^2}-\dfrac{1}{xy}\ge\dfrac{1}{4}\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\)
\(\Rightarrow0\le\dfrac{1}{x}+\dfrac{1}{y}\le4\)
\(A=\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\left(\dfrac{1}{x^2}+\dfrac{1}{y^2}-\dfrac{1}{xy}\right)=\left(\dfrac{1}{x}+\dfrac{1}{y}\right)^2\le16\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 5 2021
Ngắn gọn thì đây là 1 bài toán không giải được (min max tồn tại, nhưng không thể tìm được)
Cực trị xảy ra tại \(x=\dfrac{a}{b}\) là nghiệm của pt bậc 4:
\(7x^4+11x^3-3x^2-4x-2=0\)
Là một pt không thể phân tích về các pt bậc thấp hơn
a=2,b=4
Để giải phương trình này, ta có thể sử dụng một số phân tích như sau:
1. Trường hợp đặc biệt: Nếu (a = b), thì phương trình trở thành (a^a = a^a), điều này luôn đúng với mọi giá trị của (a).
2. Trường hợp (a = 1) hoặc (b = 1): Nếu một trong hai số là 1, thì phương trình trở thành (1^b = b^1), điều này cũng luôn đúng với mọi giá trị của (b).
3. Trường hợp (a = 2) và (b = 4): Ta thấy rằng (2^4 = 4^2), vậy đây là một giá trị thỏa mãn.
4. Trường hợp (a = 4) và (b = 2): Ta thấy rằng (4^2 = 2^4), vậy đây cũng là một giá trị thỏa mãn.
Vậy, các cặp giá trị thỏa mãn phương trình là ((a, b) = (2, 4)) và ((a, b) = (4, 2)).