Tìm số tự nhiên n để đơn thức A=3y4 chia hết cho đơn thức...
Đọc tiếp
Tìm số tự nhiên n để đơn thức A=3y4 chia hết cho đơn thức B=23yn
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 1 2018
Ta có
A : B = ( 7 x n - 1 y 5 - 5 x 3 y 4 ) : ( 5 x 2 y n ) = 7 / 5 x n - 3 y 5 - 5 - x y 4 - n
Theo đề bài đa thức A chia hết cho đơn thức B
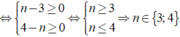
Vậy giá trị n cần tìm là n∈{3; 4}
KV
31 tháng 10 2023
Để A ⋮ B thì:
3n ≤ 9 và 2n ≥ 4
n ≤ 3 và n ≥ 2
n = 2 hoặc n = 3
CM
20 tháng 1 2017
Ta có B : C = ( 4 x 4 y 4 ) : ( x n - 1 y 4 )
Đơn thức B chia hết cho đơn thức C khi 4 ≥ n – 1 => n ≤ 5
Hay 0 < n ≤ 5
Đáp án cần chọn là: B
NV
0
TH
0
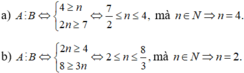
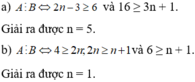
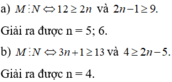
\(\dfrac{A}{B}=\dfrac{3y^4}{2^3\cdot y^n}=\dfrac{3}{8}\cdot y^{4-n}\)
Để A chia hết cho B thì \(3y^4⋮8y^n\)
=>4-n>=0
=>n<=4
mà n là số tự nhiên
nên \(n\in\left\{0;1;2;3;4\right\}\)