1 tìm x: a). 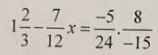 b).
b). 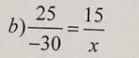
2 so sánh: 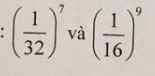
giúp mình với mình cám ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\dfrac{2024^{2023}+1}{2024^{2024}+1}\)
\(2024A=\dfrac{2024^{2024}+2024}{2024^{2024}+1}=\dfrac{\left(2024^{2024}+1\right)+2023}{2024^{2024}+1}=\dfrac{2024^{2024}+1}{2024^{2024}+1}+\dfrac{2023}{2024^{2024}+1}=1+\dfrac{2023}{2024^{2024}+1}\)
\(B=\dfrac{2024^{2022}+1}{2024^{2023}+1}\)
\(2024B=\dfrac{2024^{2023}+2024}{2024^{2023}+1}=\dfrac{\left(2024^{2023}+1\right)+2023}{2024^{2023}+1}=\dfrac{2024^{2023}+1}{2024^{2023}+1}+\dfrac{2023}{2024^{2023}+1}=1+\dfrac{2023}{2024^{2023}+1}\)
Vì \(2024>2023=>2024^{2024}>2024^{2023}\)
\(=>2024^{2024}+1>2024^{2023}+1\)
\(=>\dfrac{2023}{2024^{2023}+1}>\dfrac{2023}{2024^{2024}+1}\)
\(=>A< B\)
\(#PaooNqoccc\)

Ta có \(A=\dfrac{1}{2}+\dfrac{2}{2^2}+\dfrac{3}{2^3}+...+\dfrac{2022}{2^{2022}}+\dfrac{2023}{2^{2023}}\)
\(2A=1+\dfrac{2}{2}+\dfrac{3}{2^2}+...+\dfrac{2022}{2^{2021}}+\dfrac{2023}{2^{2022}}\)
\(2A-A=\left(1+\dfrac{2}{2}+\dfrac{3}{2^2}+...+\dfrac{2022}{2^{2021}}+\dfrac{2023}{2^{2022}}\right)-\left(\dfrac{1}{2}+\dfrac{2}{2^2}+\dfrac{3}{2^3}+...+\dfrac{2022}{2^{2022}}+\dfrac{2023}{2^{2023}}\right)\)\(A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2021}}+\dfrac{1}{2^{2022}}\) - \(\dfrac{2023}{2^{2023}}\)
Đặt B = \(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2021}}+\dfrac{1}{2^{2022}}\)
2B = \(2+1+\dfrac{1}{2}+...+\dfrac{1}{2^{2020}}+\dfrac{1}{2^{2021}}\)
2B - B = \(\left(2+1+\dfrac{1}{2}+...+\dfrac{1}{2^{2020}}+\dfrac{1}{2^{2021}}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2021}}+\dfrac{1}{2^{2022}}\right)\)B = 2 - \(\dfrac{1}{2^{2022}}\)
Suy ra A = 2 - \(\dfrac{1}{2^{2022}}\) - \(\dfrac{2023}{2^{2023}}\) < 2
Vậy A < 2
\(A=\dfrac{1}{2}+\dfrac{2}{2^{2}}+\dfrac{3}{2^{3}}+...+\dfrac{2022}{2^{2022}}+\dfrac{2023}{2^{2023}}\)
\(2A=1+\dfrac22+\dfrac3{2^2}\ +\,.\!.\!.+\ \dfrac{2022}{2^{2021}}+\dfrac{2023}{2^{2022}}\\2A-A=\left(1+\dfrac22+\dfrac3{2^2}\ +\,.\!.\!.+\ \dfrac{2022}{2^{2021}}+\dfrac{2023}{2^{2022}}\right)-\left(\dfrac12+\dfrac2{2^2}+\dfrac3{2^3}\ +\,.\!.\!.+\ \dfrac{2022}{2^{2022}}+\dfrac{2023}{2^{2023}}\right)\\A=1+\dfrac12+\dfrac1{2^3}\ +\,.\!.\!.+\ \dfrac1{2^{2021}}+\dfrac1{2^{2022}}-\dfrac{2023}{2^{2023}}\\2\left(A+\dfrac{2023}{2^{2023}}\right)=2+1+\dfrac12+\dfrac1{2^2}\ +\,.\!.\!.+\ \dfrac1{2^{2020}}+\dfrac1{2^{2021}}\\A+\dfrac{2023}{2^{2023}}=2-\dfrac1{2^{2022}}\\A=2-\dfrac1{2^{2022}}+\dfrac{2023}{2^{2023}}<2\)

\(y=\dfrac{x-1}{x^2-mx+1}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{x-1}{x^2-mx+1}=\lim\limits_{x\rightarrow-\infty}\dfrac{x-1}{x^2-mx+1}=0\)
Đồ thị có 3 tiệm cận khi đồ thị có 2 tiệm cận đứng
\(\Rightarrow x^2-mx+1\) có 2 nghiệm phân biệt khác 1
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=m^2-4>0\\1-m+1\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< -2\\m>2\end{matrix}\right.\\m\ne2\end{matrix}\right.\)

\(y=\dfrac{2x-1}{mx^2-1}\)
Để hàm số có tiệm cận đứng x=2
\(\Rightarrow mx^2-1=0\) có nghiệm x=2
\(\Rightarrow m.2^2-1=0\Rightarrow4m=1\Rightarrow m=\dfrac{1}{4}\)

\(^6\sqrt{2019} = b, ^6\sqrt{2020} = a \\ Then, A = a^3 - b^3; B = a^2 -b^2\\ \Rightarrow A > B \)

Ta có:
\(-\dfrac{9}{19}>-\dfrac{10}{19}>-\dfrac{10}{21}\\ \Rightarrow-\dfrac{9}{19}>-\dfrac{10}{21}\)

\(a,x+\frac{4}{5}-x+4=\frac{x}{3}-x-1\)
\(x+\frac{24}{5}-x=\frac{x}{3}-x-1\)
\(x+\frac{24}{5}-x-\frac{x}{3}+x+1=0\)
\(x+\frac{29}{5}-\frac{x}{3}=0\)
\(x-\frac{1}{3}x=-\frac{29}{5}\)
\(\frac{2}{3}x=-\frac{29}{5}\)
\(x=-\frac{87}{10}\)
1:
a: \(1\dfrac{2}{3}-\dfrac{7}{12}x=\dfrac{-5}{24}\cdot\dfrac{8}{-15}\)
=>\(\dfrac{5}{3}-\dfrac{7}{12}x=\dfrac{5}{15}\cdot\dfrac{8}{24}=\dfrac{1}{9}\)
=>\(\dfrac{7}{12}x=\dfrac{5}{3}-\dfrac{1}{9}=\dfrac{14}{9}\)
=>\(x=\dfrac{14}{9}:\dfrac{7}{12}=\dfrac{14}{9}\cdot\dfrac{12}{7}=2\cdot\dfrac{4}{3}=\dfrac{8}{3}\)
b: \(\dfrac{25}{-30}=\dfrac{15}{x}\)
=>\(\dfrac{15}{x}=\dfrac{5}{-6}\)
=>\(x=\dfrac{15\cdot\left(-6\right)}{5}=-3\cdot6=-18\)
2:
\(\left(\dfrac{1}{32}\right)^7=\left[\left(\dfrac{1}{2}\right)^5\right]^7=\left(\dfrac{1}{2}\right)^{35}\)
\(\left(\dfrac{1}{16}\right)^9=\left[\left(\dfrac{1}{2}\right)^4\right]^9=\left(\dfrac{1}{2}\right)^{36}\)
mà 35<36 và 1/2<1
nên \(\left(\dfrac{1}{2}\right)^{35}>\left(\dfrac{1}{2}\right)^{36}\)
=>\(\left(\dfrac{1}{32}\right)^7>\left(\dfrac{1}{16}\right)^9\)