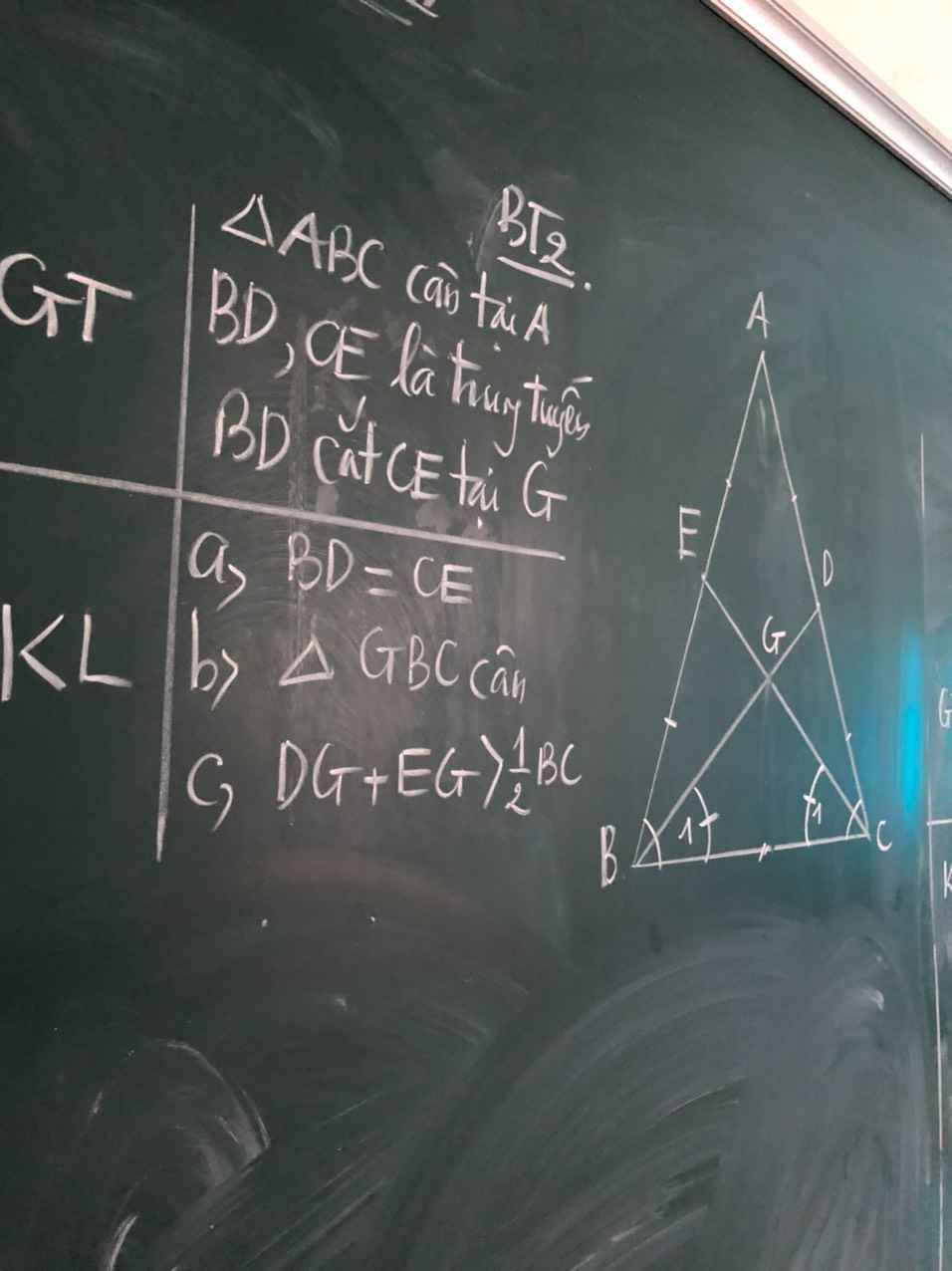Giups với ạ,tớ gấp gấp lắm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PN
0
H
7 tháng 5 2022
1)
- Phần hệ số: -5
- Phần biến: x3y
2)
- Để △ABC và △DEF bằng nhau thì cần thêm điều kiện BC=EF => △ABC = △DEF (cgc)
3)
a.
- Dấu hiệu ở đây là điểm kiểm tra môn Toán một tiết của mỗi học sinh lớp 7A.
-Mo=7
b.
x ̅= \(\dfrac{5.1+6.3+7.6+8.4+9.4+10.2}{20}=7.65\)
≈ 7.7 (điểm)
4)
a. A= 5x2y - 6xy - 2x2y + 6xy - 1
A= (5x2y - 2x2y) + (- 6xy + 6xy) -1
A= 3x2y -1
b. Thay x=2; y=-1 vào đa thức A có:
A = 3. 22. (-1) -1
A = 3. 4. (-1) -1
A= -12 - 1 = -13
Vậy giá trị của A tại x=2; y= -1 là -13
H
7 tháng 5 2022
5) A(x) + B(x)=(3x3- 5x2 - 2x + 13)+(-2x3 + 3x2 + 2x - 5)
= (3x3 -2x3) + (- 5x2 + 3x2) + (- 2x + 2x) + (13 – 5)
= x^3 – 2x^2 + 8
6)
Cho 3x-12=0
3x = 0 + 12 = 12
x = 12 : 3
x = 6
Vậy nghiệm của đa thức 3x – 12 = 6
7)
a. Trong △PRK, PK < PR
=> gK > gR (quan hệ giữa cạnh và góc đối diện)
b. Áp dụng định lý Py-ta-go vào △PRK có:
KR2 = PK2+ PR2
= 122 + 162
= 144 + 256 = 400
=> KR= 20 cm
8.
a.
Xét △OAC vuông tại A và △OBC vuông tại B có:
OC chung
gOAC = gOBC
=> △OAC = △OBC (ch-gn)
b.
gOAC = gOBC
=> OC là đường phân giác
=> CB = CA (tính chất tia phân giác của một góc)
Vì △OAC = △OBC nên OA = OB (2 cạnh tương ứng)
=> △OAB cân tại A
Ta có:
CB = CA => C ∈ đường trung trực của AB (1)
OA = OB => O ∈ đường trung trực của AB (2)
Từ (1) và (2) => OC là đường trung trực của AB.
9)
a. Xét △AHC và △MHC vuông tại H có:
HC chung
gACH=gMCH (HC là đường phân giác)
=> △AHC =△MHC (cgv-gn)
=> MC = AC (2 cạnh tương ứng)
=> △AMC cân tại C
b. Cho OM ⊥ AB tại O, MI ⊥ AC tại I
Xét △AMI vuông tại I và △MAK vuông tại K có:
AM cạnh chung
gMAI = AMK (tg MAC cân)
=> △AMI = △MAK (cgv-gn)
Ta thấy: \(\widehat{I}=\widehat{A}=\widehat{M}=\widehat{K}=90\) độ
=> AIMO là hình chữ nhật
=> OM = AI; OA = MI
Xét △OMA và △IAM có:
AM chung
OM = AI (cmt)
OA = MI (cmt)
=>△OMA =△IAM (ccc)
=>△OMA =△IAM = tg KMA
=> g OAM = g KAM (2 góc tương ứng)
=> AM hay AH là đường phân giác g OAK
Mặt khác: AH ⊥ EN => AH là đường cao △ENA
AH là đường cao đồng thời là đường phân giác => △ENA cân
=> AH cũng là đường trung trực
Do đó: EH = HN nên H là trung điểm EN
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 8 2021
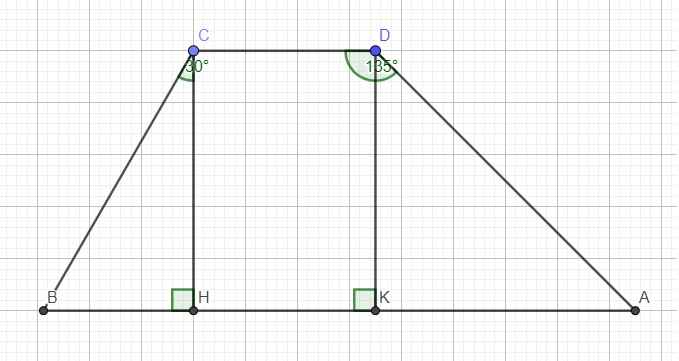
Từ D kẻ đường vuông góc DK (K thuộc AB) \(\Rightarrow CDKH\) là hình chữ nhật
\(\Rightarrow\left\{{}\begin{matrix}HK=CD=3,5\left(m\right)\\CH=DK=5\left(m\right)\end{matrix}\right.\)
Ta có:\(\widehat{KDA}=135^0-90^0=45^0\)
Trong tam giác vuông BCH:
\(cos\widehat{BCH}=\dfrac{CH}{BC}\Rightarrow BC=\dfrac{CH}{cos\widehat{BCH}}=\dfrac{5}{cos30^0}=\dfrac{10\sqrt{3}}{3}\left(m\right)\)
\(\Rightarrow BH=\sqrt{BC^2-CH^2}=\dfrac{5\sqrt{3}}{3}\left(m\right)\)
Trong tam giác vuông ADK:
\(\widehat{KAD}=90^0-\widehat{KDA}=45^0\Rightarrow\widehat{KAD}=\widehat{KDA}\Rightarrow\Delta ADK\) vuông cân tại K
\(\Rightarrow AK=DK=5\left(m\right)\)
\(\Rightarrow AD=\sqrt{AK^2+DK^2}=5\sqrt{2}\left(m\right)\)
\(AB=BH+HK+KA=\dfrac{51+10\sqrt{3}}{6}\left(m\right)\)
Chu vi: \(AB+CD+BC+AD\approx27,7\left(m\right)\)
Diện tích: \(S=\dfrac{1}{2}\left(AB+CD\right).CH\approx37,2\left(m^2\right)\)
Giải giúp tớ với ạ, tớ cần gấp lắm
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 7 2021
\(=\left(\dfrac{\sqrt{5}\left(\sqrt{3}-2\right)}{\sqrt{3}-2}+\dfrac{\sqrt{6}\left(\sqrt{3}+\sqrt{2}\right)}{\sqrt{3}+\sqrt{2}}-\dfrac{\sqrt{6}-\sqrt{5}}{\left(\sqrt{6}-\sqrt{5}\right)\left(\sqrt{6}+\sqrt{5}\right)}\right):\sqrt{\dfrac{5}{2}}\)
\(=\left(\sqrt{5}+\sqrt{6}-\sqrt{6}+\sqrt{5}\right):\dfrac{\sqrt{5}}{\sqrt{2}}\)
\(=2\sqrt{5}.\dfrac{\sqrt{2}}{\sqrt{5}}=2\sqrt{2}\)
28 tháng 7 2021
a) Ta có: \(\left(\dfrac{\sqrt{15}-\sqrt{20}}{\sqrt{3}-2}+\dfrac{3\sqrt{2}+2\sqrt{3}}{\sqrt{3}+\sqrt{2}}-\dfrac{1}{\sqrt{6}+\sqrt{5}}\right):\sqrt{\dfrac{5}{2}}\)
\(=\left(\sqrt{5}+\sqrt{6}-\sqrt{6}+\sqrt{5}\right):\dfrac{\sqrt{10}}{2}\)
\(=2\sqrt{5}\cdot\dfrac{2}{\sqrt{10}}=2\sqrt{2}\)
MN
19 tháng 3 2022
\(\dfrac{x}{27}=\dfrac{2}{9}-\dfrac{1}{3}\Rightarrow\dfrac{x}{27}=-\dfrac{1}{9}\Rightarrow\dfrac{x}{27}=\dfrac{-3}{27}\Rightarrow x=27\)
HN
19 tháng 3 2022
\(\dfrac{x}{27}=\dfrac{2}{9}-\dfrac{1}{3}=-\dfrac{1}{9}\Rightarrow x=-\dfrac{1}{9}.27=-3\).
21 tháng 8 2021
Có \(tanC=\dfrac{AB}{AC}\Leftrightarrow tan30^0=\dfrac{AB}{10}\Leftrightarrow AB=\dfrac{10\sqrt{3}}{3}\approx5,8\left(cm\right)\)
\(BC=\sqrt{AB^2+AC^2}=\dfrac{20\sqrt{3}}{3}\approx11,5\left(cm\right)\)
\(\widehat{B}=90^0-\widehat{C}=60^0\)
NK
1
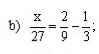
a: ta có: \(AE=EB=\dfrac{AB}{2}\)
\(AD=DC=\dfrac{AC}{2}\)
mà AB=AC
nên AE=EB=AD=DC
Xét ΔEBC và ΔDCB có
EB=DC
\(\widehat{EBC}=\widehat{DCB}\)(ΔABC cân tại A)
BC chung
Do đó: ΔEBC=ΔDCB
=>BD=CE
b: Ta có: ΔEBC=ΔDCB
=>\(\widehat{ECB}=\widehat{DBC}\)
=>\(\widehat{GBC}=\widehat{GCB}\)
=>ΔGBC cân tại G
c: Xét ΔABC có
BD,CE là các đường trung tuyến
BD cắt CE tại G
Do đó: G là trọng tâm của ΔABC
=>\(BG=\dfrac{2}{3}BD;CG=\dfrac{2}{3}CE\)
Vì \(BG=\dfrac{2}{3}BD\)
nên \(DG=\dfrac{1}{2}BG\)
Vì \(CG=\dfrac{2}{3}CE\)
nên \(EG=\dfrac{1}{2}CG\)
Xét ΔGBC có GB+GC>BC
=>\(2\left(EG+GD\right)>BC\)
=>\(GE+GD>\dfrac{BC}{2}\)