Cho tam giác ABC, gócA=90 độ, AB=6cm, góc B=60 độ
a) Tính AC, BC
b)Tính độ dài phân giác BD(D\(\in\)AC)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC vuông ở A, theo định lý Pi-ta-go ta được :
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\left(cm\right)\)
Ta có : AD là phân giác \(\widehat{BAC}\)
\(\Rightarrow\dfrac{BD}{DC}=\dfrac{AB}{AC}\)
hay \(\dfrac{BD}{DC}=\dfrac{6}{8}\)
\(\Rightarrow\dfrac{BD}{6}=\dfrac{DC}{8}=\dfrac{BD+DC}{6+8}=\dfrac{10}{14}=\dfrac{5}{7}\)
\(\Rightarrow BD=\dfrac{5}{7}.6=\dfrac{30}{7}\left(cm\right)\)
\(\Rightarrow DC=\dfrac{5}{7}.8=\dfrac{40}{7}\left(cm\right)\)
Hình bạn tự kẻ nhé!
Xét tam giác ABC vuông tại A có:
AB2 + AC2 = BC2 ( định lý Pytago )
=> 62 + 82 = BC2
<=> 36 + 64 = BC2
<=> 100 = BC2
<=> BC = 10 (cm) ( vì BC > 0 )
Xét tam giác ABC có: BD là đường pg của tam giác ABC
=> DA / DC = AB / BC
=> DA / ( DA + DC ) = AB/ ( BC + AB )
<=> DA / AC = 3/8
<=> AD / 8 = 3/8
<=> AD = 3 (cm)
Vậy AD = 3 cm.

Bài 2:
a: Đây là tam giác vuông
b: Đây ko là tam giác vuông


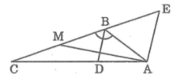

Suy ra tam giác ABE đều ⇒ AB = BE = EA = 6 (cm) (1)
Khi đó: CE = BC + BE = 12 + 6 = 18 (cm)
Tam giác ACE có AE // BD nên suy ra:
![]()

a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{ACB}+60^0=90^0\)
hay \(\widehat{ACB}=30^0\)(1)
Xét ΔABC có \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\left(30^0< 60^0< 90^0\right)\)
nên AB<AC<BC
b) Xét ΔABD vuông tại A và ΔKBD vuông tại K có
BD chung
\(\widehat{ABD}=\widehat{KBD}\)(BD là tia phân giác của \(\widehat{ABK}\))
Do đó: ΔABD=ΔKBD(cạnh huyền-góc nhọn)
c) Ta có: BD là tia phân giác của \(\widehat{ABC}\)(gt)
nên \(\widehat{ABD}=\widehat{DBC}=\dfrac{\widehat{ABC}}{2}=\dfrac{60^0}{2}=30^0\)(2)
Từ (1) và (2) suy ra \(\widehat{DBC}=\widehat{DCB}\)
Xét ΔDBC có \(\widehat{DBC}=\widehat{DCB}\)(cmt)
nên ΔDBC cân tại D(Định lí đảo của tam giác cân)
Xét ΔBDK vuông tại K và ΔCDK vuông tại K có
DB=DC(ΔDBC cân tại D)
DK chung
Do đó: ΔBDK=ΔCDK(Cạnh huyền-cạnh góc vuông)
Suy ra: BK=CK(hai cạnh tương ứng)
hay K là trung điểm của BC(Đpcm)
a. tám giác ABC có A=90, B=60 => C=30
trong 1 tam giác vuông, cạnh đối diện với góc 30 độ thì =1/2 cạnh huyền
=> 2AB=BC hay BC=12
áp dụng đlý pytago vào ABC, ta tính đc AC=\(6\sqrt{3}\)
b. tam giác ABC có BD là tia phân giác góc B =>\(\frac{AD}{DC}=\frac{AB}{BC}< =>\frac{AD}{AB}=\frac{DC}{BC}=>\frac{AD+DC}{AB+BC}=\frac{AC}{6+12}=\frac{6\sqrt{3}}{18}\)
=>\(\frac{AD}{AB}=\frac{6\sqrt{3}}{18}=>AD=\frac{6\sqrt{3}.6}{18}=2\sqrt{3}\)
áp dụng đlý pytago vào ABD => BD=\(4\sqrt{3}\)