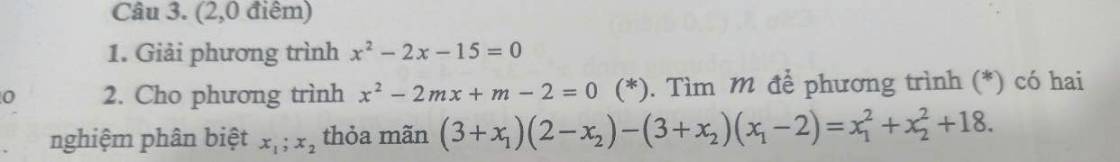mọi người giúp em với ạ !
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HK
1
10 tháng 12 2021
Câu 1.
Khi mở khóa K:
\(I_m=I_1=0,4A\)
Khi đóng khóa K:
\(I_m=I_1+I_2=0,6\Rightarrow I_2=0,2A\)
\(U_1=0,4\cdot5=2V\)
\(\Rightarrow U_2=U_1=2V\)
\(\Rightarrow U=U_1=U_2=2V\)
\(R_2=\dfrac{U_2}{I_2}=\dfrac{2}{0,2}=10\Omega\)
6 tháng 3 2022
a: Thay x=0 và y=5 vào (d), ta được:
(m-2)x0+m=5
=>m=5
c: Để hai đườg song song thì m-2=2
hay m=4
J
1
5 tháng 12 2023
Câu 10:
a: ĐKXĐ: \(\left\{{}\begin{matrix}x\notin\left\{2;-1\right\}\\y\ne-5\end{matrix}\right.\)
\(A=\dfrac{y+5}{x^2-4x+4}\cdot\dfrac{x^2-4}{x+1}\cdot\dfrac{x-2}{y+5}\)
\(=\dfrac{y+5}{y+5}\cdot\dfrac{\left(x^2-4\right)}{x^2-4x+4}\cdot\dfrac{x-2}{x+1}\)
\(=\dfrac{\left(x^2-4\right)\cdot\left(x-2\right)}{\left(x+1\right)\left(x^2-4x+4\right)}\)
\(=\dfrac{\left(x+2\right)\left(x-2\right)\cdot\left(x-2\right)}{\left(x+1\right)\left(x-2\right)^2}=\dfrac{x+2}{x+1}\)
b: \(A=\dfrac{x+2}{x+1}\)
=>A không phụ thuộc vào biến y
Khi x=1/2 thì \(A=\left(\dfrac{1}{2}+2\right):\left(\dfrac{1}{2}+1\right)=\dfrac{5}{2}:\dfrac{3}{2}=\dfrac{5}{2}\cdot\dfrac{2}{3}=\dfrac{5}{3}\)
Câu 12:
a: \(A=\dfrac{x}{x+3}+\dfrac{2x}{x-3}+\dfrac{9-3x^2}{x^2-9}\)
\(=\dfrac{x}{x+3}+\dfrac{2x}{x-3}+\dfrac{9-3x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{x\left(x-3\right)+2x\left(x+3\right)+9-3x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{x^2-3x+2x^2+6x+9-3x^2}{\left(x+3\right)\left(x-3\right)}\)
\(=\dfrac{3x+9}{\left(x+3\right)\left(x-3\right)}=\dfrac{3\left(x+3\right)}{\left(x+3\right)\left(x-3\right)}=\dfrac{3}{x-3}\)
b: Khi x=1 thì \(A=\dfrac{3}{1-3}=\dfrac{3}{-2}=-\dfrac{3}{2}\)
\(x+\dfrac{1}{3}=\dfrac{10}{3}\)
=>\(x=\dfrac{10}{3}-\dfrac{1}{3}\)
=>\(x=\dfrac{9}{3}=3\left(loại\right)\)
Vậy: Khi x=3 thì A không có giá trị
c: \(B=A\cdot\dfrac{x-3}{x^2-4x+5}\)
\(=\dfrac{3}{x-3}\cdot\dfrac{x-3}{x^2-4x+5}\)
\(=\dfrac{3}{x^2-4x+5}\)
\(x^2-4x+5=x^2-4x+4+1=\left(x-2\right)^2+1>=1\forall x\) thỏa mãn ĐKXĐ
=>\(B=\dfrac{3}{x^2-4x+5}< =\dfrac{3}{1}=3\forall x\) thỏa mãn ĐKXĐ
Dấu '=' xảy ra khi x-2=0
=>x=2
B
4
HK
1
12 tháng 12 2021
Đề 1:
Bài 1:
\(a,=\sqrt{\left(\sqrt{7}+1\right)^2}-\left|-1+\sqrt{7}\right|=\sqrt{7}+1-\sqrt{7}+1=2\\ b,=2\sqrt{2}-4\sqrt{2}-5\sqrt{2}+\dfrac{\sqrt{2}}{2}=\dfrac{\sqrt{2}}{2}-7\sqrt{2}=\dfrac{-13\sqrt{2}}{\sqrt{2}}\)
Bài 2:
\(PT\Leftrightarrow\sqrt{\left(x-\dfrac{1}{2}\right)^2}=\dfrac{1}{2}\Leftrightarrow\left|x-\dfrac{1}{2}\right|=\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}+\dfrac{1}{2}=1\\x=-\dfrac{1}{2}+\dfrac{1}{2}=0\end{matrix}\right.\)
Bài 3:
\(a,M=\dfrac{a-2\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{2\sqrt{a}}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}=\dfrac{2\left(\sqrt{a}-1\right)^2}{\left(\sqrt{a}-1\right)^2\left(\sqrt{a}+1\right)}=\dfrac{2}{\sqrt{a}+1}\\ b,M< 1\Leftrightarrow\dfrac{2}{\sqrt{a}+1}-1< 0\Leftrightarrow\dfrac{1-\sqrt{a}}{\sqrt{a}+1}< 0\\ \Leftrightarrow1-\sqrt{a}< 0\left(\sqrt{a}+1>0\right)\\ \Leftrightarrow a>1\)
1) \(x^2-2x-15=0\)
\(\Delta=\left(-2\right)^2-4\cdot1\cdot-15=64>0\)
Phương trình có 2 nghiệm phân biệt
\(x_1=\dfrac{2+\sqrt{64}}{2\cdot1}=5\)
\(x_2=\dfrac{2-\sqrt{64}}{2\cdot1}=-3\)
2) \(x^2-2mx+m-2=0\)
\(\Delta=\left(-2m\right)^2-4\cdot1\cdot\left(m-2\right)=4m^2-4m+8=\left(2m-1\right)^2+7>0\forall m\)
Theo vi-ét:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-\left(-2m\right)}{1}=2m\\x_1x_2=\dfrac{m-2}{1}=m-2\end{matrix}\right.\)
Ta có: \(\left(3+x_1\right)\left(2-x_2\right)-\left(3+x_2\right)\left(x_1-2\right)=x^2_1+x^2_2+18\)
\(\Leftrightarrow6-3x_2+2x_1-x_1x_2-\left(-6+3x_1-2x_2+x_1x_2\right)=x^2_1+x^2_2+18\)
\(\Leftrightarrow6-3x_2+2x_1-x_1x_2+6-3x_1+2x_2-x_1x_2=\left(x_1+x_2\right)^2-2x_1x_2+18\)
\(\Leftrightarrow12-3\left(x_1+x_2\right)+2\left(x_1+x_2\right)-2x_1x_2=\left(x_1+x_2\right)^2-2x_1x_2+18\)
\(\Leftrightarrow12-\left(x_1+x_2\right)=\left(x_1+x_2\right)^2+18\)
\(\Leftrightarrow12-2m=\left(2m\right)^2+18\)
\(\Leftrightarrow12-2m=4m^2+18\)
\(\Leftrightarrow4m^2+2m+6=0\)
\(\Leftrightarrow m\in\varnothing\)
Vậy không có m thỏa mãn