Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
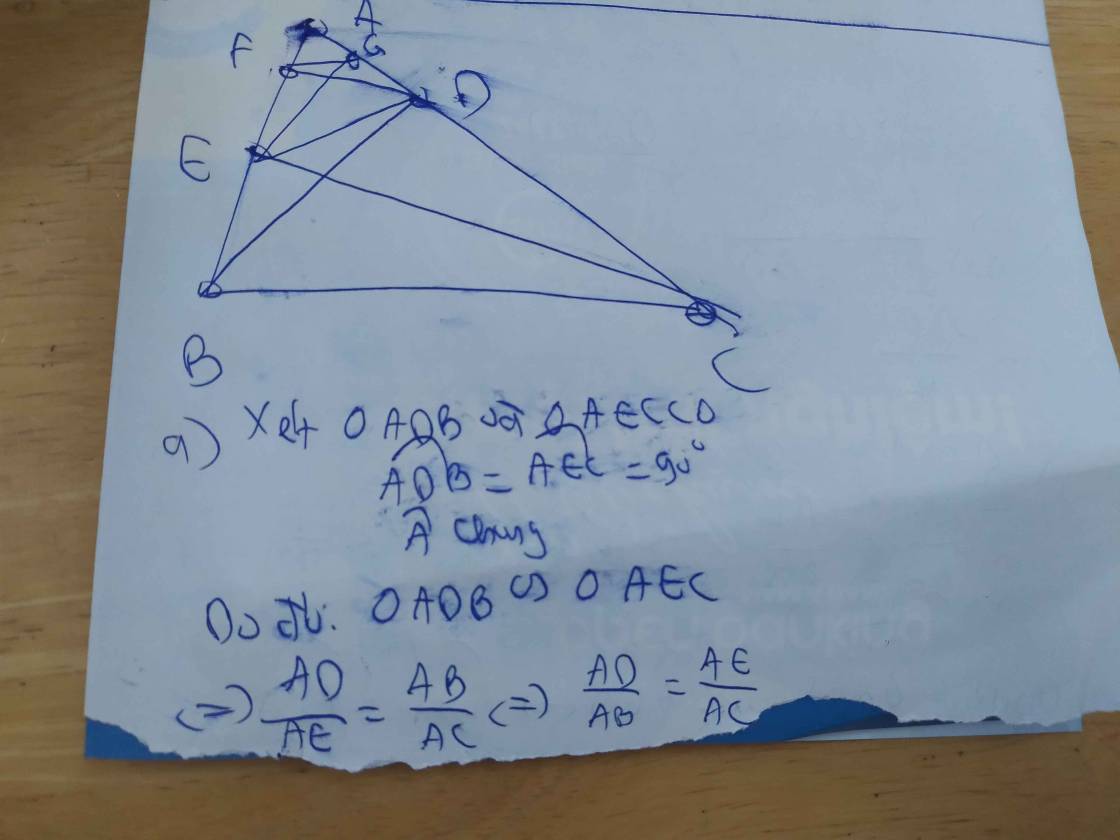
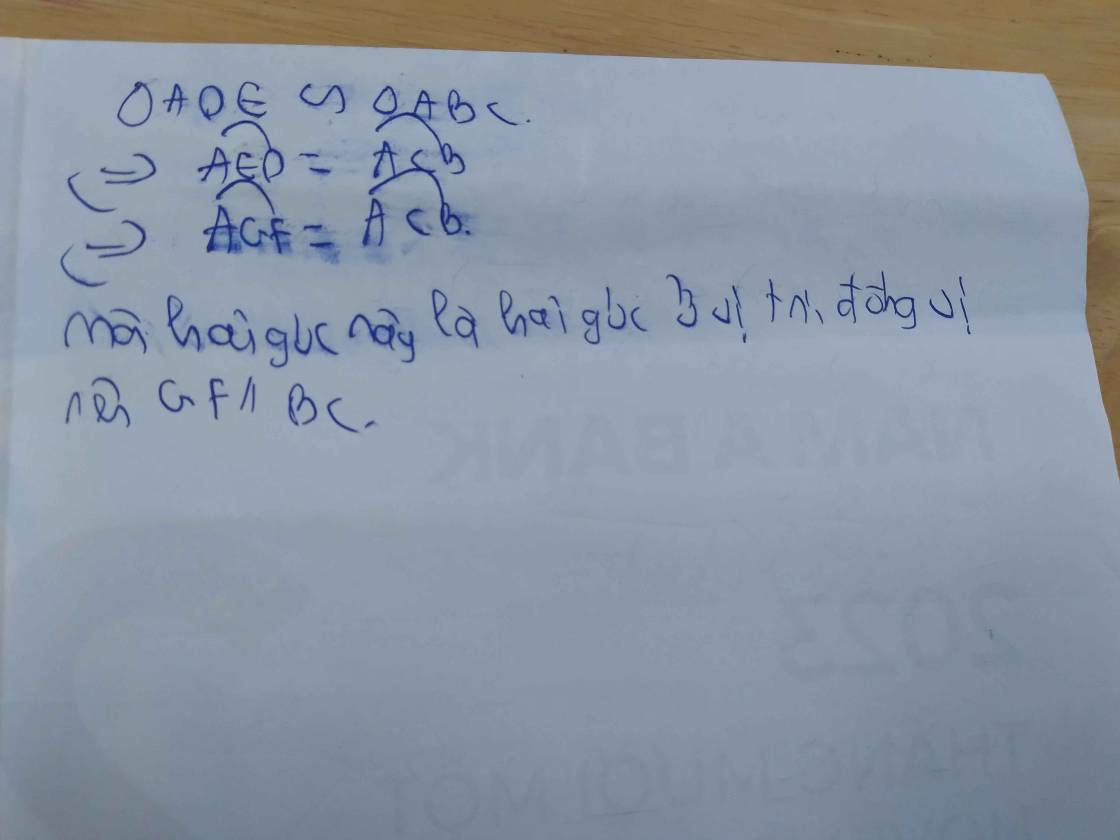
a) Xét ΔABD vuông tại D và ΔACE vuông tại E có
\(\widehat{BAD}\) chung
Do đó: ΔABD∼ΔACE(g-g)
b) Xét ΔEHB vuông tại E và ΔDHC vuông tại D có
\(\widehat{EHB}=\widehat{DHC}\)(hai góc đối đỉnh)
Do đó: ΔEHB∼ΔDHC(g-g)
Suy ra: \(\dfrac{HE}{HD}=\dfrac{HB}{HC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(BH\cdot HD=CH\cdot HE\)(đpcm)
a) Xét ΔABD vuông tại D và ΔACE vuông tại E có
\(\widehat{BAD}\) chung
Do đó: ΔABD\(\sim\)ΔACE(g-g)
Bạn tự vẽ hình nhé :^
a) Xét tam giác ABD và tam giác ACE có :
góc ADB = góc ACE ( vì cùng bằng 90 độ )
góc BAC chung
=> tam giác ABD đồng dạng với tam giác ACE ( g.g)
b) Vì tam giác ABD đồng dạng với tam giác ACE (cmt)
=> \(\frac{AB}{AC}=\frac{AD}{AE}\)( định nghĩa tam giác đồng dạng)
Xét tam giác ADE và tam giác ABC có
\(\frac{AD}{AE}=\frac{AB}{AC}\)(cmt)
\(\widehat{BAC}\)chung
\(\Rightarrow\) tam giác ADE đồng dạng với tam giác ABC ( c.g.c)
Còn câu c là gì vậy ạ ?
a)Xét ADB và tam giác AEC ta có:
`hat{AEC}=hat{ADB}=90^o`(gt)
`hat{A}` chung
`=>Delta ADB~Delta AEC(gg)`
b)Vì `Delta ADB~Delta AEC(gg)`
`=>(AB)/(AC)=(AE)/(AD)`
`=>DeltaADE~Delta ABC(cgc)`
c)
a) Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{A}\) chung
Do đó: ΔADB∼ΔAEC(g-g)
b) Ta có: ΔADB∼ΔAEC(cmt)
nên \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
hay \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét ΔADE và ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)(cmt)
\(\widehat{A}\) chung
Do đó: ΔADE∼ΔABC(c-g-c)
ADE ∽