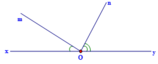
B1: Cho góc bẹt xOy. Trên cùng một nửa mặt phẳng bờ xy, vẽ các tia Om và On sao cho xOm=yOn và <90*. Gọi Oz là tia phân giác của góc mOn. Chứng minh rằng Oz _|_ xy.
B2: Cho góc AOB = 40*. Vẽ tia Oc là tia đối của tia OA. Tính góc COD, biết rằng:
a) OD _|_ Ob, các tia Od và OA thuộc hai nửa mặt phẳng đối nhau bờ Ob
b)OD _|_ Ob, các tia OD và OA thuộc cùng một nửa mặt phẳng bở OB
E CẦN GẤP MỌI NGƯỜI GIÚP E VS Ạ
CÓ HÌNH HOẶC HÌNH MINH HỌA THÌ CÀNG TỐT Ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+) Ta có: x O m ^ = 30 0 , y O n ^ = 2 x O m ^ = 2.30 0 = 60 0 Vì x O m ^ + m O y ^ = x O y ^ = 180 0 (hai góc kề bù) => m O y ^ = 180 0 − x O m ^ = 180 0 − 30 0 = 150 0 +) Xét trên nửa mặt phẳng có bờ chứa tia Oy, có : y O n ^ < y O m ^ (vì 0 ° < 60 ° < 150 ° ) => Tia On nằm giữa hai tia Oy và Om ⇒ m O n ^ + n O y ^ = m O y ^ = 150 0 ⇒ m O n ^ + 60 0 = 150 0 ⇒ m O n ^ = 150 0 − 60 0 ⇒ m O n ^ = 90 0 ⇒ O m ⊥ O n . |

Đáp án là D
Vì tia On là tia phân giác của ∠yOm nên ∠yOm = 2.∠yOn = 2. 70 0 = 140 0
Lại có xOy là góc bẹt nên ∠xOm và ∠yOm là hai góc kề bù
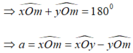
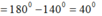
Vậy a = 40 0

Bài làm
Ta có: \(\widehat{xOy}=\widehat{xOm}+\widehat{yOn}+\widehat{mOz}+\widehat{zOn}\)
Mà \(\widehat{xOm}=\widehat{yOn}=2\widehat{xOm}\)
Oz là tia phân giác của \(\widehat{mOn}\)
=> \(\widehat{mOz}=\widehat{zOn}=2\widehat{mOz}\)
=> \(\widehat{xOy}=2\widehat{xOm}+2\widehat{mOz}\)
Hay \(180^0=2\widehat{xOm}+2\widehat{mOz}\)
=> \(180^0=2(\widehat{xOm}+\widehat{mOz})\)
=> \(\widehat{xOm}+\widehat{mOz}=180^0:2\)
=> \(\widehat{xOm}+\widehat{mOz}=90^0\)
Hay \(\widehat{xOz}=90^0\)
=> \(Oz\perp xy\)
Vậy \(Oz\perp xy\)( đpcm )
# Học tốt #

\(A)\)
\(B)\)
Theo đề ra: Góc xOy là góc bẹt => Góc xOy = 180 độ
Góc xOm = 60 độ
=> Góc xOy > góc xOm => Tia Om nằm giữa hai tia Ox và Oy
Ta có: mOy = xOy - xOm
mOy = 180 độ - 60 độ
mOy = 120 độ
Ta có: mOn = yOn - mOy
mOn = 150 độ - 120 độ
mOn = 30 độ
\(C)\)
Ta có: xOn = xOm - mOn
xOn = 60 độ - 30 độ
xOn = 30 độ
=> Góc xOn = góc mOn
=> Tia On là tia phân giác của góc xOm

Vì Om và On là hai tia nằm giữa hai tia Ox và Oy
=>mOnˆ=xOyˆ−xOmˆ−yOn^
⇔mOnˆ=1800−2yOnˆ
Mà Ot là tia phân giác của góc mOn
⇔tOn^=1/2(1800−2yOn^)
⇔tOnˆ=900−yOnˆ
Vì Ot là tia phân giác của góc mOn
=>tOyˆ=tOnˆ+yOnˆtOy^
⇔zOyˆ=900−yOnˆ
⇔tOyˆ=900
⇔Ot⊥xy
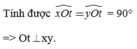
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)