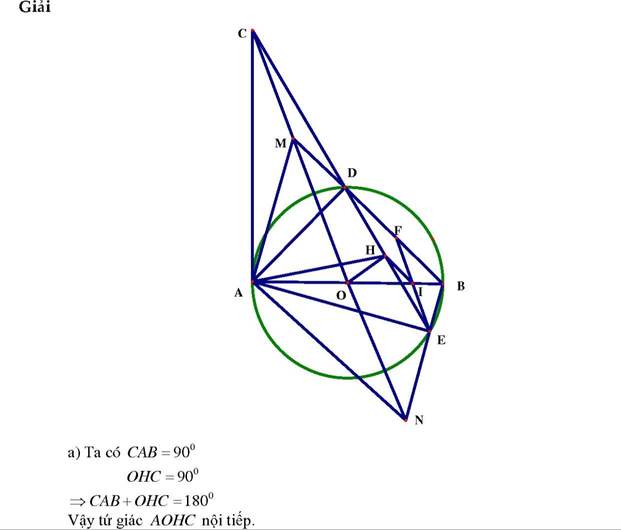
Cho AB là một đường kính cố định của đường tròn (O). Qua điểm A vẽ đường thẳng d vuông góc với AB. Từ một điểm E bất kì trên đường thẳng d vẽ tiếp tuyến với đường tròn (O) (C là tiếp điểm, C khác A). Vẽ đường tròn (K) đi qua C và tiếp xúc với đường thẳng d tại E, vẽ đường kính EF của đường tròn (K). Gọi M là trung điểm của OE. Chứng minh rằng:
- Điểm M thuộc đường tròn (K).
- Đường thẳng đi qua F và vuông góc với BE luôn đi qua một điểm cố định khi E thay đổi trên đường thẳng d.