Gieo một con xúc sắc 4 lần. Tìm xác suất của biến cố A:" Mặt 3 chấm xuất hiện đúng một lần"
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 2 2018
Gọi B i là biến cố “ mặt 3 chấm xuất hiện lần thứ i” với i =1;2; 3; 4
Khi đó: B i ¯ là biến cố “ Mặt 3 chấm không xuất hiện lần thứ i”
Ta có: A = B 1 ¯ . B 2 . B 3 . B 4 ∪ B 1 . B 2 ¯ . B 3 . B 4 ∪ B 1 . B 2 . B 3 ¯ . B 4 ∪ B 1 . B 2 . B 3 . B 4 ¯
Suy ra :
P A = P B 1 P B 2 P B 3 P B 4 + P B 1 P B 2 P B 3 P B 4 + P B 1 P B 2 P B 3 P B 4 + P B 1 P B 2 P B 3 P B 4
Mà : P ( B i ) = 1 6 ⇒ P ( B i ¯ ) = 1 − 1 6 = 5 6 .
Do đó: P ( A ) = 4. 1 6 3 . 5 6 = 5 324 .
Chọn đáp án A
CM
29 tháng 5 2017
Gọi A i là biến cố “ mặt 4 chấm xuất hiện lần thứ i” với i = 1; 2; 3; 4.
Khi đó: A i là biến cố “ Mặt 4 chấm không xuất hiện lần thứ i”
Và P ( A i ¯ ) = 1 − P ( A i ) = 1 − 1 6 = 5 6
Ta có: A ¯ là biến cố: “ không có mặt 4 chấm xuất hiện trong 4 lần gieo”
Và A ¯ = A 1 ¯ . A 2 ¯ . A 3 ¯ . A 4 ¯ . Vì các A i ¯ độc lập với nhau nên ta có:
P ( A ¯ ) = P ( A 1 ¯ ) . P ( A 2 ¯ ) . P ( A 3 ¯ ) . P ( A 4 ¯ ) = 5 6 4
Vậy P ( A ) = 1 − P ( A ¯ ) = 1 − 5 6 4 .
Chọn đáp án A.
20 tháng 2 2023
a: \(\Omega=\left\{1;2;3;4;5;6\right\}\)
=>n(omega)=6
A={1;4}
=>n(A)=2
=>P(A)=2/6=1/3
b: B={3;4;5;6}
=>n(B)=4
=>P(B)=4/6=2/3
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 12 2020
a. Có 3 mặt nguyên tố: 2,3,5 nên xác suất xuất hiện số nguyên tố ở mỗi lần gieo là \(\dfrac{3}{6}=\dfrac{1}{2}\)
Xác suất 2 lần đều xuất hiện số nguyên tố: \(\dfrac{1}{2}.\dfrac{1}{2}=\dfrac{1}{4}\)
b. Xác suất để lần 1 xuất hiện mặt 6 chấm: \(\dfrac{1}{6}\)
c. Xác suất ít nhất 1 lần xuất hiện mặt 6 chấm: \(\dfrac{2.6-1}{36}=\dfrac{11}{36}\)
d. Xác suất ko lần nào xuất hiện 6 chấm: \(1-\dfrac{11}{36}=\dfrac{25}{36}\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2022
Không gian mẫu: \(6.6=36\)
a.
Lần thứ nhất có 1 khả năng thỏa mãn (3 chấm)
Lần thứ 2 bất kì => có 6 khả năng
\(\Rightarrow1.6=6\) khả năng để lần thứ nhất xuất hiện mặt 3 chấm
Xác suất: \(P=\dfrac{6}{36}=\dfrac{1}{6}\)
b.
Xác suất để cả 2 lần đều ko xuất hiện mặt 2 chấm là: \(\dfrac{5}{6}.\dfrac{5}{6}=\dfrac{25}{36}\)
Xác suất để ít nhất 1 lần xuất hiện mặt 2 chấm: \(1-\dfrac{25}{36}=\dfrac{11}{36}\)
c.
Các trường hợp có số chấm thuận lợi: (1;1);(1;2);(1;3);(1;4);(2;1);(2;2);(2;3);(3;1);(3;2);(4;1) có 10 trường hợp
Xác suất: \(P=\dfrac{10}{36}=\dfrac{5}{18}\)
22 tháng 12 2022
Thầy có thể giải thích hơn về câu a và câu b của bài này được không ạ?
H9
HT.Phong (9A5)
CTVHS
8 tháng 5 2023
Câu 1: Gieo 1 đồng tiền cân đối và đồng chất 2 lần
\(\Rightarrow n\left(\Omega\right)=2^2=4\)
Gọi A là biến cố cả hai lần xuất hiện mặt sấp
\(\Rightarrow A=\left\{SS\right\}\Rightarrow n\left(A\right)=1\)
Vậy \(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{1}{4}\)
Chọn B
Câu 2: Số phần tử không gian mẫu: \(n\left(\Omega\right)=6\)
Gọi biến cố A: “Số chấm là số nguyên tố xuất hiện”
\(A=\left\{2;3;5\right\}\)
\(\Rightarrow n\left(A\right)=3\)
Vậy \(P\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=\dfrac{3}{6}=\dfrac{1}{2}\)
Chọn A
8 tháng 3 2023
a: \(\Omega=\left\{1;2;3;4;5;6\right\}\Leftrightarrow n\left(\Omega\right)=6\)
\(A=\left\{2;5\right\}\)
=>P(A)=2/6=1/3
b: B={1;5}
=>n(B)=2
=>P(B)=2/6=1/3
HQ
Hà Quang Minh
Giáo viên
28 tháng 9 2023
Không gian mẫu trong trò chơi trên là tập hợp \(\Omega = \left\{ {(i,j)|i,j = 1,2,3,4,5,6} \right\}\)trong đó (i,j) là kết quả “Lần thứ nhất xuất hiện mặt i chấm, lần thứ hai xuất hiện mặt j chấm”. Vậy \(n(\Omega ) = \;36.\)
a) Gọi A là biến cố “Tổng số chấm xuất hiện trong hai lần gieo không bé hơn 10”.
Các kết quả có lợi cho A là: (4; 6) (5;5) (5;6) (6; 4) (6;5) (6;6). Vậy \(n(A) = \;6.\)
Vậy xác suất của biến cố A là \(P(A) = \;\frac{{n(A)}}{{n(\Omega )}} = \frac{6}{{36}} = \frac{1}{6}.\)
b) Gọi B là biến cố “Mặt 1 chấm xuất hiện ít nhất một lần”.
Các kết quả có lợi cho B là: (1; 1) (1 : 2) (1 : 3) (1; 4) (1;5) (1; 6) (2 ; 1) (3;1) (4; 1) (5;1) (6;1). Vậy \(n(B) = \;11.\)
Vậy xác suất của biến cố B là: \(P(B) = \;\frac{{n(B)}}{{n(\Omega )}} = \frac{{11}}{{36}}.\)
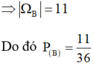
Đây giống với xác suất đại học hơn thì phải, cấp 3 hình như người ta ko cho dạng này (công thức Bernoulli)
\(P=C_4^1.\left(\dfrac{1}{6}\right)^1.\left(\dfrac{5}{6}\right)^{4-1}\)
Vâng anh! Thể nào em tính không ra đáp án như đề.
Anh ơi! Giả sử 2 gieo con xúc sắc 4 lần không gian mẫu là tính như nào ạ anh