Biết a,b,c khác 0. CMR: \(\dfrac{a^2}{\left(b-c\right)^2}+\dfrac{b^2}{\left(c-a\right)^2}+\dfrac{c^2}{\left(a-b\right)^2}\ge2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
nguyễn thị hương giang
31 tháng 1
Đúng(2)
Những câu hỏi liên quan
20 tháng 12 2020
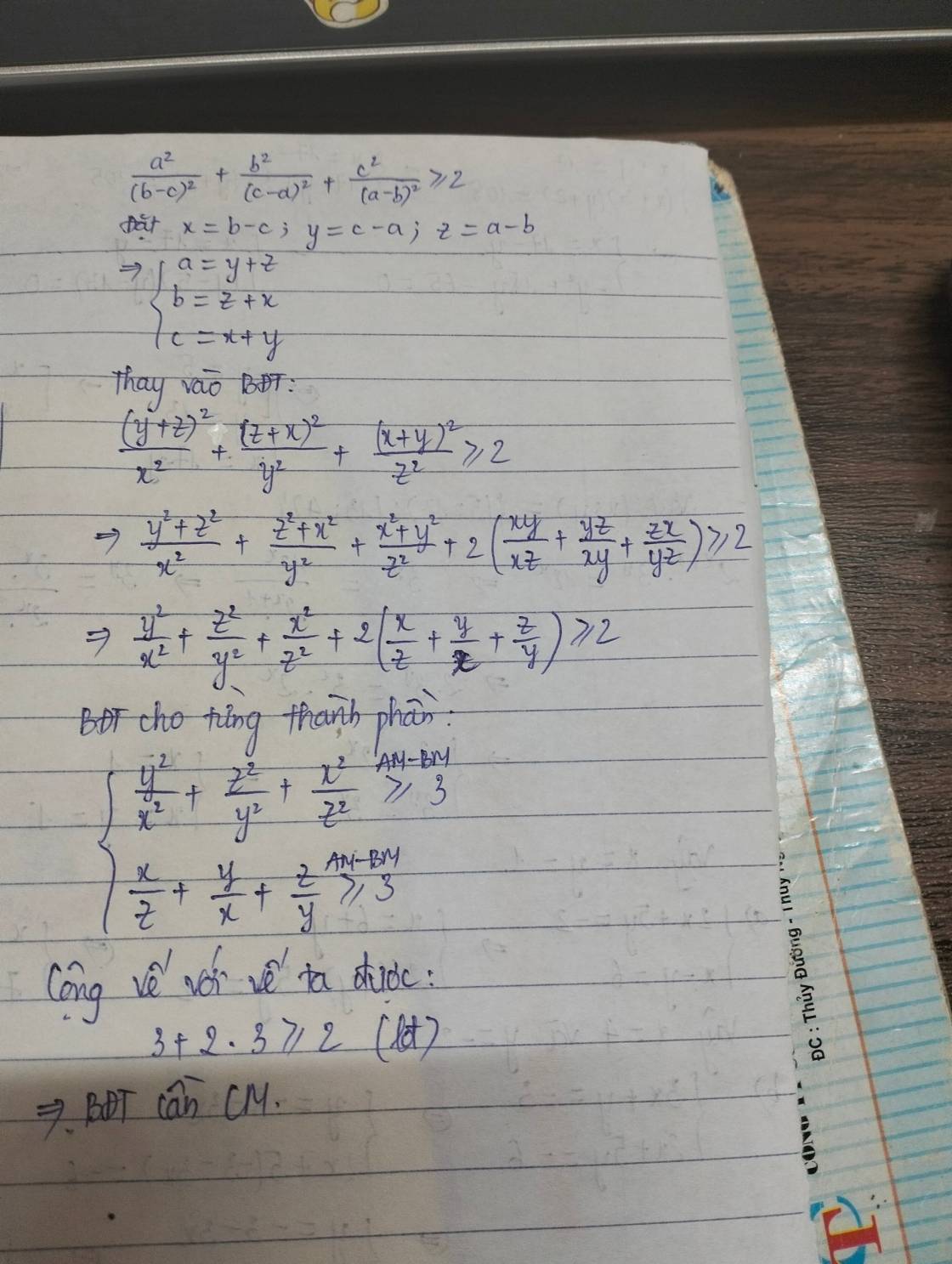
BĐT đã cho tương đương với:
\(\left(\dfrac{a}{b-c}+\dfrac{b}{c-a}+\dfrac{c}{a-b}\right)^2-2\left[\dfrac{ab}{\left(b-c\right)\left(c-a\right)}+\dfrac{bc}{\left(c-a\right)\left(a-b\right)}+\dfrac{ca}{\left(a-b\right)\left(b-c\right)}\right]\ge2\left(\cdot\right)\).
Mặt khác ta có: \(\dfrac{ab}{\left(b-c\right)\left(c-a\right)}+\dfrac{bc}{\left(c-a\right)\left(a-b\right)}+\dfrac{ca}{\left(a-b\right)\left(b-c\right)}=\dfrac{ab\left(a-b\right)+bc\left(b-c\right)+ca\left(c-a\right)}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}=\dfrac{-\left(a-b\right)\left(b-c\right)\left(c-a\right)}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}=-1\).
Do đó \(\left(\cdot\right)\Leftrightarrow\left(\dfrac{a}{b-c}+\dfrac{b}{c-a}+\dfrac{c}{a-b}\right)^2\ge0\) (luôn đúng).
BĐT đã cho dc c/m.
26 tháng 7 2018
T đề nghị ban EDOGAWA CONAN không dùng nick k\này hỏi rồi lấy nick chính trả lời và tự tick nữa. T biết hai cậu là 1 mà không muốn nói thôi.
P/s:Nếu thế nữa t sẽ báo phynit.
26 tháng 7 2018
Đặt : \(x=\dfrac{a+b}{a-b}\) ; \(y=\dfrac{b+c}{b-c}\) ; \(z=\dfrac{c+a}{c-a}\)
Ta có : \(\left(x+1\right)\left(y+1\right)\left(z+1\right)=\left(x-1\right)\left(y-1\right)\left(z-1\right)\)
\(\Leftrightarrow xy+yz+zx=-1\)
Mà \(\left(x+y+z\right)^2\ge0\)
\(\Leftrightarrow x^2+y^2+z^2+2\left(xy+yz+zx\right)\ge0\)
\(\Leftrightarrow x^2+y^2+z^2\ge2\)
\(\Rightarrow\dfrac{\left(a+b\right)^2}{\left(a-b\right)^2}+\dfrac{\left(b+c\right)^2}{\left(b-c\right)^2}+\dfrac{\left(c+a\right)^2}{\left(c-a\right)^2}\ge2\left(đpcm\right)\)
C
16 tháng 1 2023
`VT = (b-c)/((a-b)(a-c)) + (c-a)/((b-c)(b-a)) +(a-b)/((c-a)(c-b)) = 2/(a-b) + 2/(b-c) + 2/(c-a)`
`=-((a-b-a+c)/((a-b)(a-c))+(b-c-b+a)/((b-c)(b-a))+(c-a-c+b)/((c-a)(c-b)))`
`=-((a-b)/((a-b)(a-c))-(a-c)/((a-b)(a-c))+(b-c)/((b-c)(b-a))-(b-a)/((b-c)(b-a))+(c-a)/((c-a)(c-b))-(c-b)/((c-a)(c-b)))`
`= 1/(c-a)+1/(a-b)+1/(a-b)+1/(b-c)+1/(b-c)+1/(c-a)`
`=2/(a-b)+2/(b-c)+2/(c-a)=VP(đpcm)`
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2022
1.
BĐT cần chứng minh tương đương:
\(\left(ab-1\right)\left(bc-1\right)\left(ca-1\right)\ge\left(a^2-1\right)\left(b^2-1\right)\left(c^2-1\right)\)
Ta có:
\(\left(ab-1\right)^2=a^2b^2-2ab+1=a^2b^2-a^2-b^2+1+a^2+b^2-2ab\)
\(=\left(a^2-1\right)\left(b^2-1\right)+\left(a-b\right)^2\ge\left(a^2-1\right)\left(b^2-1\right)\)
Tương tự: \(\left(bc-1\right)^2\ge\left(b^2-1\right)\left(c^2-1\right)\)
\(\left(ca-1\right)^2\ge\left(c^2-1\right)\left(a^2-1\right)\)
Do \(a;b;c\ge1\) nên 2 vế của các BĐT trên đều không âm, nhân vế với vế:
\(\left[\left(ab-1\right)\left(bc-1\right)\left(ca-1\right)\right]^2\ge\left[\left(a^2-1\right)\left(b^2-1\right)\left(c^2-1\right)\right]^2\)
\(\Rightarrow\left(ab-1\right)\left(bc-1\right)\left(ca-1\right)\ge\left(a^2-1\right)\left(b^2-1\right)\left(c^2-1\right)\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c\)
Câu 2 em kiểm tra lại đề có chính xác chưa
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 4 2022
2.
Câu 2 đề thế này cũng làm được nhưng khá xấu, mình nghĩ là không thể chứng minh bằng Cauchy-Schwaz được, phải chứng minh bằng SOS
Không mất tính tổng quát, giả sử \(c=max\left\{a;b;c\right\}\)
\(\Rightarrow\left(c-a\right)\left(c-b\right)\ge0\) (1)
BĐT cần chứng minh tương đương:
\(\dfrac{1}{a}-\dfrac{a+b}{bc+a^2}+\dfrac{1}{b}-\dfrac{b+c}{ac+b^2}+\dfrac{1}{c}-\dfrac{c+a}{ab+c^2}\ge0\)
\(\Leftrightarrow\dfrac{b\left(c-a\right)}{a^3+abc}+\dfrac{c\left(a-b\right)}{b^3+abc}+\dfrac{a\left(b-c\right)}{c^3+abc}\ge0\)
\(\Leftrightarrow\dfrac{c\left(b-a\right)+a\left(c-b\right)}{a^3+abc}+\dfrac{c\left(a-b\right)}{b^3+abc}+\dfrac{a\left(b-c\right)}{c^3+abc}\ge0\)
\(\Leftrightarrow c\left(b-a\right)\left(\dfrac{1}{a^3+abc}-\dfrac{1}{b^3+abc}\right)+a\left(c-b\right)\left(\dfrac{1}{a^3+abc}-\dfrac{1}{c^3+abc}\right)\ge0\)
\(\Leftrightarrow\dfrac{c\left(b-a\right)\left(b^3-a^3\right)}{\left(a^3+abc\right)\left(b^3+abc\right)}+\dfrac{a\left(c-b\right)\left(c^3-a^3\right)}{\left(a^3+abc\right)\left(c^3+abc\right)}\ge0\)
\(\Leftrightarrow\dfrac{c\left(b-a\right)^2\left(a^2+ab+b^2\right)}{\left(a^3+abc\right)\left(b^3+abc\right)}+\dfrac{a\left(c-b\right)\left(c-a\right)\left(a^2+ac+c^2\right)}{\left(a^3+abc\right)\left(c^3+abc\right)}\ge0\)
Đúng theo (1)
Dấu "=" xảy ra khi \(a=b=c\)
27 tháng 12 2020
\(\left(a^2-bc\right)\left(b-abc\right)=\left(b^2-ca\right)\left(a-abc\right)\)
\(\Leftrightarrow a^2b+ab^2c^2-a^3bc-b^2c=b^2a+a^2bc^2-ca^2-ab^3c\)
\(\Leftrightarrow a^2b-ab^2-b^2c+ca^2=a^2bc^2-ab^3c+a^3bc-ab^2c^2\)
\(\Leftrightarrow\left(a-b\right)\left(ab+bc+ca\right)=abc\left(a-b\right)\left(a+b+c\right)\)
\(\Leftrightarrow ab+bc+ca=abc\left(a+b+c\right)\Leftrightarrow a+b+c=\dfrac{ab+bc+ca}{abc}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\left(đpcm\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 1
Trước hết ta có:
\(\dfrac{ab}{\left(b-c\right)\left(c-a\right)}+\dfrac{ac}{\left(b-c\right)\left(a-b\right)}+\dfrac{bc}{\left(c-a\right)\left(a-b\right)}\)
\(=\dfrac{ab\left(a-b\right)+bc\left(b-c\right)+ca\left(c-a\right)}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}\)
\(=\dfrac{ab\left(a-b\right)+b^2c-a^2c+ac^2-bc^2}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}\)
\(=\dfrac{ab\left(a-b\right)-c\left(a-b\right)\left(a+b\right)+c^2\left(a-b\right)}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}\)
\(=\dfrac{\left(a-b\right)\left(ab-ac-bc+c^2\right)}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}=\dfrac{\left(a-b\right)\left[a\left(b-c\right)-c\left(b-c\right)\right]}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}\)
\(=\dfrac{\left(a-b\right)\left(b-c\right)\left(a-c\right)}{\left(a-b\right)\left(b-c\right)\left(c-a\right)}=-1\)
Do đó:
\(\left(\dfrac{a}{b-c}\right)^2+\left(\dfrac{b}{c-a}\right)^2+\left(\dfrac{c}{a-b}\right)^2-2+2\)
\(=\left(\dfrac{a}{b-c}\right)^2+\left(\dfrac{b}{c-a}\right)^2+\left(\dfrac{c}{a-b}\right)^2+2\left(\dfrac{ab}{\left(b-c\right)\left(c-a\right)}+\dfrac{ac}{\left(a-b\right)\left(b-c\right)}+\dfrac{bc}{\left(c-a\right)\left(a-b\right)}\right)+2\)
\(=\left(\dfrac{a}{b-c}+\dfrac{b}{c-a}+\dfrac{c}{a-b}\right)^2+2\ge2\) (đpcm)
AH
Akai Haruma
Giáo viên
31 tháng 8 2023
Lời giải:
Đặt $\frac{a+b}{a-b}=x; \frac{b+c}{b-c}=y; \frac{c+a}{c-a}=z$. Khi đó:
$xy+yz+xz=\frac{(a+b)(b+c)}{(a-b)(b-c)}+\frac{(a+b)(c+a)}{(a-b)(c-a)}+\frac{(b+c)(c+a)}{(b-c)(c-a)}$
$=\frac{(a+b)(b+c)(c-a)+(b+c)(c+a)(a-b)+(c+a)(a+b)(b-c)}{(a-b)(b-c)(c-a)}=-1$
Suy ra:
$(\frac{a+b}{a-b})^2+(\frac{b+c}{b-c})^2+(\frac{c+a}{c-a})^2=x^2+y^2+z^2=(x+y+z)^2-2(xy+yz+xz)$
$=(x+y+z)^2+2\geq 2$
Ta có đpcm.
16 tháng 11 2018
\(\frac{a^4}{\left(a^2-b^2+c^2\right)\left(a^2+b^2-c^2\right)}=\frac{a^4}{\left[\left(a-b\right)\left(a+b\right)+c^2\right]\left[\left(a-c\right)\left(a+c\right)+b^2\right]}\)
\(\frac{a^4}{\left[-c\left(a-b\right)+c^2\right]\left[-b\left(a-c\right)+b^2\right]}=\frac{a^4}{4bc\left(b+c\right)^2}=\frac{a^4}{4a^2bc}\)
Tương tự với 2 phân thức còn lại, ta cũng có : \(\frac{b^4}{b^4-\left(c^2-a^2\right)^2}=\frac{b^4}{4ab^2c};\frac{c^4}{c^4-\left(a^2-b^2\right)^2}=\frac{c^4}{4abc^2}\)
\(VT=\frac{a^4}{4a^2bc}+\frac{b^4}{4ab^2c}+\frac{c^4}{4abc^2}=\frac{a^4bc+ab^4c+abc^4}{4a^2b^2c^2}=\frac{abc\left(a^3+b^3+c^3\right)}{4a^2b^2c^2}\)
\(VT=\frac{a^3+b^3+c^3}{4abc}\)
Mà \(a+b+c=0\) nên \(a^3+b^3+c^3=3abc\) ( tự cm )
\(\Rightarrow\)\(VT=\frac{3abc}{4abc}=\frac{3}{4}\) ( đpcm )
Chúc bạn học tốt ~