khai trien: (xm+yn).(yn-xm)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
Để $A,B$ đồng dạng thì: \(\left\{\begin{matrix} m-3=6\\ 2=n\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} m=9\\ n=2\end{matrix}\right.\)

A B C O M N X Y P Q R S
Gọi MO,NO cắt đường thẳng BC lần lượt tại R,S.
Xét \(\Delta XAC\): M là trung điểm cạnh AC, MO || AX vì cùng vuông góc AC, suy ra MO đi qua trung điểm XC
Ta có R là trung điểm XC, MN || XC vì MN là đường trung bình \(\Delta ABC\), suy ra \(M\left(CXRN\right)=-1\)
Tương tự thì \(N\left(YBSM\right)=-1\)
Do đó \(M\left(CXRN\right)=N\left(YBSM\right)\) hay \(M\left(QPON\right)=N\left(QPOM\right)\)
Suy ra P,O,Q thẳng hàng.

Ta có \(\frac{a}{x}=\frac{b}{y}=\frac{c}{z}=\frac{am}{xm}=\frac{bn}{yn}=\frac{cp}{zp}=\frac{am-bn+cp}{xm-yn+zp}\) (đpcm)
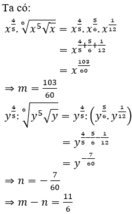
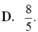
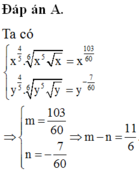
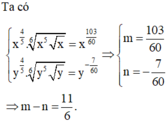
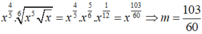
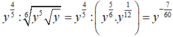
a) 3n + 5 chia hết cho n+1
ta có 3n+5=3n+3+2=3.(n+1)+2
vì 3.(n+1) chia hết cho n+1 =>để 3.(n+1)+2 chia hết cho n+1 thì 2 phải chia hết cho n+1
=> n+1 thuộc {1;2} =>n thuộc {0;1}
b) 3n + 5 chia hết cho 2n+1
ta có: 3n+5=2n+n+1+4=(2n+1)+(n+4)
vì 2n+1 chia hết cho 2n+1 =>để (2n+1)+(n+4) chia hết cho 2n+1 thì (n+4) phải chia hết cho 2n +1
=>n+4>=2n+1
n+1+3 >=n+n+1
3>=n =>n thuộc {0;1;2;3}
* với n=0 =>n+4=4 ; 2n+1=1 vậy n+4 chia hết cho 2n+1 =>n=0 thỏa mãn
* với n=1 =>n+4=4 ; 2n+1=1 vậy n+4 chia hết cho 2n+1 =>n=0 thỏa mãn
c) 2n + 3 chia hết cho 5 - 2n
để 5-2n >=0 =>5-2n >=5-5 =>2n <=5 => n thuộc{0;1;2}
* với n=0 =>2n+3 =3 ; 5-2n=5 không thỏa mãn
*với n=1 =>2n+3=5 ;5 -2n=3 không thỏa mãn
*với n=2 =>2n+3=7 ; 5-2n =1 thỏa mãn vì 2n + 3 chia hết cho 5 - 2n
vậy n=3