Giả sử a, b là các số dương thỏa a2 + b2 = 7ab. Chứng minh \(2\log_2\left(\dfrac{a+b}{3}\right)=\log_2a+\log_2b\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
25 tháng 5 2023
Lời giải:
Áp dụng BĐT Cauchy-Schwarz và AM-GM:
$M=\frac{b^2+c^2}{a^2}+a^2(\frac{1}{b^2}+\frac{1}{c^2})$
$\geq \frac{b^2+c^2}{a^2}+a^2.\frac{4}{b^2+c^2}$
$=(\frac{b^2+c^2}{a^2}+\frac{a^2}{b^2+c^2})+\frac{3a^2}{b^2+c^2}$
$\geq \sqrt{\frac{b^2+c^2}{a^2}.\frac{a^2}{b^2+c^2}}+\frac{3(b^2+c^2)}{b^2+c^2}$
$=2+3=5$
Vậy $M_{\min}=5$
11 tháng 5 2016
\(D=\frac{\log_2\left(2a^2\right)+\left(\log_2a\right)a^{\log_2\left(\log_2a+1\right)}+\frac{1}{2}\log^2_2a^4}{\log_2a^3\left(3\log_2a+1\right)+1}=\frac{1+2\log_2a+\log_2a\left(\log_2a+1\right)+8\log^2_2a}{3\log_2a.\left(3\log_2a+1\right)+1}\)
\(=\frac{9\log^2_2a+3\log_2a+1}{9\log^2_2a+3\log_2a+1}=1\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 8 2021
Ta chứng minh BĐT sau cho các số dương:
\(x^5+y^5\ge xy\left(x^3+y^3\right)\)
\(\Leftrightarrow x^5-x^4y+y^5-xy^4\ge0\)
\(\Leftrightarrow\left(x^4-y^4\right)\left(x-y\right)\ge0\)
\(\Leftrightarrow\left(x-y\right)^2\left(x+y\right)\left(x^2+y^2\right)\ge0\) (đúng)
Áp dụng:
\(\dfrac{a^5+b^5}{ab\left(a+b\right)}\ge\dfrac{ab\left(a^3+b^3\right)}{ab\left(a+b\right)}=\dfrac{a^3+b^3}{a+b}=a^2-ab+b^2\)
Tương tự và cộng lại:
\(VT\ge2\left(a^2+b^2+c^2\right)-\left(ab+bc+ca\right)=2-\left(ab+ca+ca\right)\)
\(VT\ge4-\left(ab+bc+ca\right)-2=4\left(a^2+b^2+c^2\right)-\left(ab+bc+ca\right)-2\)
\(VT\ge4\left(ab+bc+ca\right)-\left(ab+bc+ca\right)-2=3\left(ab+bc+ca\right)-2\) (đpcm)
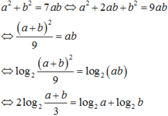
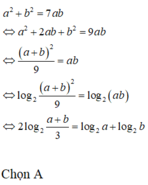
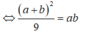
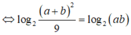
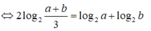
\(a^2+b^2=7ab\Leftrightarrow a^2+b^2+2ab=9ab\)
\(\Leftrightarrow\left(a+b\right)^2=9ab\Leftrightarrow\dfrac{\left(a+b\right)^2}{9}=ab\)
\(\Leftrightarrow\left(\dfrac{a+b}{3}\right)^2=ab\)
Lấy logarit cơ số 2 hai vế:
\(log_2\left(\dfrac{a+b}{3}\right)^2=log\left(ab\right)\)
\(\Leftrightarrow2log_2\left(\dfrac{a+b}{3}\right)=log_2a+log_2b\)
https://hoc24.vn/cau-hoi/.8778209332689
giúp em ạ