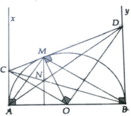
Cho nửa(O), đường kính AB =2R. vẽ bán kính OC vuông góc với AB. M là 1 điểm chuyển động trên cung BC nhỏ, AM cắt OC tại P
a) Tìm vị trí điểm M để PO=PM. Tính diện tích AMB theo R
b) Tìm vị trí điểm M để MB=MP. Tính diện tích AMB theo R
c) Gọi I là tâm đường tròn ngoại tiếp tam giác CPM. Khi M chuyển động I chạy trên đường nào ?

a.
AB là đường kính nên \(\widehat{AMB}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{AMB}=90^0\)
\(\Rightarrow M\) và O cùng nhìn BP dưới 1 góc vuông nên tứ giác OBMP nội tiếp
Mà \(PO=PM\Rightarrow\widehat{PBO}=\widehat{PBM}\)
\(\Rightarrow\Delta_VPBO=\Delta_VPBM\left(ch-gn\right)\) (có cạnh huyền PB chung)
\(\Rightarrow BM=OB=R\)
Vậy M nằm ở vị trí sao cho \(BM=R\) thì \(PO=PM\)
Áp dụng Pitago: \(AM=\sqrt{AB^2-BM^2}=\sqrt{\left(2R\right)^2-R^2}=R\sqrt{3}\)
\(\Rightarrow S_{ABM}=\dfrac{1}{2}AM.BM=\dfrac{R^2\sqrt{3}}{2}\)
b.
\(MB=MP\Rightarrow\Delta MBP\) vuông cân tại M
\(\Rightarrow\widehat{BPM}=45^0\)
Theo câu a ta có OBMP nội tiếp \(\Rightarrow\widehat{BOM}=\widehat{BPM}=45^0\) (cùng chắn BM)
\(\Rightarrow\widehat{BOM}=\dfrac{1}{2}\widehat{BOC}\) \(\Rightarrow M\) là điểm chính giữa cung BC
Khi đó kẻ \(MH\perp AB\Rightarrow\Delta MOH\) vuông cân tại H (tam giác cân có góc đáy bằng 45 độ)
\(\Rightarrow MH=\dfrac{OM}{\sqrt{2}}=\dfrac{R\sqrt{2}}{2}\)
\(S_{AMB}=\dfrac{1}{2}MH.AB=R^2\sqrt{2}\)
c.
Qua P kẻ đường thẳng song song AB cắt BC tại D
\(\Rightarrow DP\perp CP\Rightarrow\Delta CPD\) nội tiếp đường tròn đường kính CD (1)
\(\widehat{MPD}=\widehat{MAB}\) (đồng vị), mà \(\widehat{MAB}=\widehat{MCB}\) (cùng chắn BM)
\(\Rightarrow\widehat{MPD}=\widehat{MCB}\)
\(\Rightarrow\) Tứ giác MCPD nội tiếp (2 góc bằng nhau cùng chắn MD) (2)
(1);(2) \(\Rightarrow\) M,C,P cùng thuộc đường tròn đường kính CD
Hay tâm I của tam giác CPM nằm trên đường thẳng BC khi M di động trên cung BC