Cho tam giác chọn ABC. Kẻ BH vuông góc với AC ( H \(\in\)AC ), kẻ CK vuông góc với AB ( K \(\in\) AB). Hãy so sánh góc ABH và góc ACK.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
6 tháng 9 2019
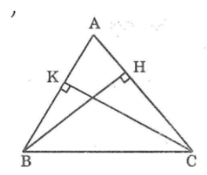
Tam giác ABH vuông tại H
⇒ ∠(ABH) +∠A =90o (tính chất tam giác vuông)
⇒∠(ABH) =90o - ∠A (1)
Tam giác ACK vuông tại K
⇒∠(ACK) +∠A =90o(tính chất tam giác vuông)
⇒∠(ACK) =90o-∠A (2)
từ (1) và (2) suy ra: ∠(ACK) =∠(ABH)
QT
0
5 tháng 2 2022
a: \(\widehat{ABH};\widehat{ACK}\) là các góc phụ với A
b: Vì \(\widehat{ABH}+\widehat{A}=90^0\)
mà \(\widehat{ACK}+\widehat{A}=90^0\)
nên \(\widehat{ABH}=\widehat{ACK}\)
\(\widehat{BIK}=\widehat{CIH}\)(hai góc đối đỉnh)
UN
0
12 tháng 11 2021
Tam giác ABH vuông tại H
⇒ ∠(ABH) +∠A =90o (tính chất tam giác vuông)
⇒∠(ABH) =90o - ∠A (1)
Tam giác ACK vuông tại K
⇒∠(ACK) +∠A =90o(tính chất tam giác vuông)
⇒∠(ACK) =90o-∠A (2)
từ (1) và (2) suy ra: ∠(ACK) =∠(ABH)
LM
Lê Minh Vũ
CTVHS
12 tháng 11 2021
Tam giác ABH vuông tại H
\(\Rightarrow\)\(ABH+A=90^o\) (tính chất tam giác vuông)
\(\Rightarrow\)\(ABH=90-A\)\(\left(1\right)\)
Tam giác ACK vuông tại K
\(\Rightarrow\)\(ACK+A=90^0\)(tính chất tam giác vuông)
\(ACK=90^o-A\)\(\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\)\(ABH=ACK\)