Câu 3 (2,0 điểm) 1) Hai người làm chung một công việc hết 8 giờ. Nếu người thứ nhất làm 25% công việc, người thứ hai làm 25% công việc thì tổng cộng hết 9 giờ. Hỏi mỗi người lâm riêng thi sau bao lâu hoàn thành công việc đó?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


bài này mình không biết làm nhưng bạn hãy kết bạn với mình và kích điểm hỏi hỏi đáp cho mình nha

trong 1 giờ ba người thợ làm được số công việc là:
1:6=1/6 (công việc)
trong 1 giờ người thứ nhất làm được số phần công việc là:
1:12=1/12 (công việc)
trong 1 giờ người thứ hai làm được số phần công việc là:
1:16=1/16 (công việc)
trong 1 giờ người thứ ba làm xong số phần công việc là:
1/6-(1/12+1/16=1/48 (công việc)
Vậy một mình người thứ ba làm xong công việc thì sẽ hoàn thành trong:
1:1/48=48 (giờ)

Gọi tg người thứ nhất làm riêng và hoàn thành cv là x
tg người thứ 2 làn riêng hoàn thành cv là y (x,y>0)
vi 2 người cùng làm chung trong 8h thì xong cv nên \(\dfrac{8}{x}+\dfrac{8}{y}=1\) (1)
vì nếu người thứ nhất làm trong 1h30p=3/2h và ng thứ 2 lm tiếp 3h thì đc 25% cv nên \(\dfrac{3}{2x}+\dfrac{3}{y}=\dfrac{1}{4}\) (2)
từ 1 và 2 ta có hpt \(\left\{{}\begin{matrix}\dfrac{8}{x}+\dfrac{8}{y}=1\\\dfrac{3}{2x}+\dfrac{3}{y}=\dfrac{1}{4}\end{matrix}\right.< =>\left\{{}\begin{matrix}x=12\left(tm\right)\\y=24\left(tm\right)\end{matrix}\right.\)( tự giải hệ và kết luận)

Gọi x(giờ) và y(giờ) lần lượt là thời gian người thứ nhất và người thứ hai hoàn thành công việc khi làm một mình(Điều kiện: x>16; y>16)
Trong 1 giờ, người thứ nhất làm được: \(\dfrac{1}{x}\)(công việc)
Trong 1 giờ, người thứ hai làm được: \(\dfrac{1}{y}\)(công việc)
Trong 1 giờ, hai người thợ làm được: \(\dfrac{1}{16}\)(công việc)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\)(1)
Vì khi người thứ nhất làm trong 3 giờ, người thứ 2 làm trong 6 giờ thì hoàn thành được 25% công việc nên ta có phương trình:
\(\dfrac{3}{x}+\dfrac{6}{y}=\dfrac{1}{4}\)(2)
Từ (1) và (2) ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\\\dfrac{3}{x}+\dfrac{6}{y}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{x}+\dfrac{3}{y}=\dfrac{3}{16}\\\dfrac{3}{x}+\dfrac{6}{y}=\dfrac{1}{4}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{-3}{y}=\dfrac{-1}{16}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=48\\\dfrac{1}{x}=\dfrac{1}{16}-\dfrac{1}{y}=\dfrac{1}{16}-\dfrac{1}{48}=\dfrac{1}{24}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=24\\y=48\end{matrix}\right.\)(thỏa ĐK)
Vậy: Người thợ thứ nhất cần 24 giờ để hoàn thành công việc khi làm một mình
Người thợ thứ hai cần 48 giờ để hoàn thành công việc khi làm một mình
Gọi thời gian để người thứ nhất và người thứ hai một mình hoàn thành công việc lần lượt là x (giờ) và y (giờ). (Điều kiện x, y > 16).
⇒ Trong một giờ, người thứ nhất làm được 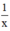 (công việc); người thứ hai làm được
(công việc); người thứ hai làm được 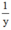 (công việc).
(công việc).
+ Cả hai người cùng làm sẽ hoàn thành công việc trong 16 giờ nên ta có phương trình 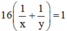
+ Người thứ nhất làm trong 3 giờ, người thứ hai làm trong 6 giờ thì hoàn thành 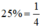 công việc nên ta có phương trình
công việc nên ta có phương trình 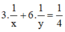
Vậy ta có hệ phương trình 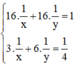
Đặt 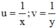 , hệ phương trình trở thành:
, hệ phương trình trở thành:
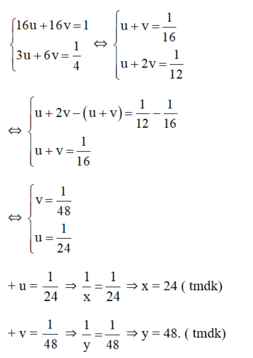

Gọi thời gian làm 1 mình xong công việc của 2 người thợ lần lượt là x>0 và y>0 giờ
Trong 1h hai người lần lượt làm được: \(\dfrac{1}{x}\) và \(\dfrac{1}{y}\) phần công việc
Do đó ta có pt: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{18}\)
Trong 8h người thứ nhất làm được: \(\dfrac{8}{x}\) phần công việc
Trong 6h người thứ 2 làm được: \(\dfrac{6}{y}\) phần công việc
Ta có pt: \(\dfrac{8}{x}+\dfrac{6}{y}=\dfrac{2}{5}\) (với \(\dfrac{2}{5}=40\%\))
Từ đó ta có hệ: \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{18}\\\dfrac{8}{x}+\dfrac{6}{y}=\dfrac{2}{5}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{30}\\\dfrac{1}{y}=\dfrac{1}{45}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=30\\y=45\end{matrix}\right.\)
Gọi thời gian làm riêng hoàn thành công việc của người thứ nhất là x(giờ), của người thứ hai là y(giờ)
(Điều kiện: x>0 và y>0 và x<>36 và y<>36)
Trong 1 giờ, người thứ nhất làm được \(\dfrac{1}{x}\)(công việc)
Trong 1 giờ, người thứ hai làm được \(\dfrac{1}{y}\)(công việc)
Trong 1 giờ, hai người làm được \(\dfrac{1}{8}\)(công việc)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{8}\left(1\right)\)
Thời gian để người thứ nhất làm được 25% công việc là:
\(x\cdot25\%=0,25x\left(giờ\right)\)
Thời gian để người thứ hai làm được 25% công việc là:
y*25%=0,25y(giờ)
Nếu người thứ nhất làm 25% công việc và người thứ hai làm 25% công việc thì hết 9 giờ nên ta có:
0,25x+0,25y=9
=>x+y=36
=>x=36-y
\(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{8}\)
=>\(\dfrac{1}{36-y}+\dfrac{1}{y}=\dfrac{1}{8}\)
=>\(\dfrac{y+36-y}{y\left(36-y\right)}=\dfrac{1}{8}\)
=>y(36-y)=288
=>\(36y-y^2-288=0\)
=>\(y^2-36y+288=0\)
=>\(\left[{}\begin{matrix}y=24\left(nhận\right)\\y=12\left(nhận\right)\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=12\\x=24\end{matrix}\right.\)
Vậy: Thời gian người thứ nhất và người thứ hai hoàn thành công việc khi làm một mình có thể là (12 giờ;24 giờ) hoặc (24 giờ; 12 giờ)
*Đã có người trả lời*=>Bấm để xem đáp án