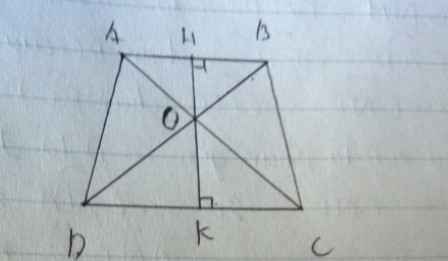
Hình thang ABCD có O là giao điểm của hai đường chéo. Tính diện tích hình thang ABCD. Biết diện tích hình tam giác AOD là 10 cm2 và diện tích tam giác DOC là 20cm2.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


-Chắc bạn học Toán IQ quá.
AB//CD \(\Rightarrow S_{BAD}=S_{ABC}\Rightarrow S_{BAD}-S_{OAB}=S_{ABC}-S_{OAB}\Rightarrow S_{OAD}=S_{OBC}=10cm^2\)\(\dfrac{OB}{OD}=\dfrac{S_{OAB}}{S_{OAD}}=\dfrac{6}{10}=\dfrac{3}{5}\)
\(\dfrac{S_{OBC}}{S_{ODC}}=\dfrac{OB}{OD}=\dfrac{3}{5}\)
\(\Rightarrow S_{ODC}=\dfrac{5}{3}S_{OBC}=\dfrac{5}{3}.10=\dfrac{50}{3}\left(cm^2\right)\)
\(S_{ABCD}=S_{OAB}+S_{OAD}+S_{OBC}+S_{ODC}=6+10+10+\dfrac{50}{3}=\dfrac{128}{3}\left(cm^2\right)\)

\(ABssCD\Rightarrow\dfrac{AB}{CD}=\dfrac{OB}{OD}=\dfrac{OA}{OC}=\dfrac{2}{3}\)
a)\(S_{AOD}=\dfrac{1}{2}OA.OD.sinAOB\)
\(S_{BOC}=\dfrac{1}{2}OB.OC.sinBOC\)
\(\Rightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{OA.OD}{OB.OC}\) vì \(\widehat{AOD}=\widehat{BOC}\Rightarrow sinAOD=sinBOC\)
\(\Leftrightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{2}{3}.\dfrac{3}{2}=1\)
b) vì \(ABssCD\Rightarrow\dfrac{OH}{OK}=\dfrac{2}{3}\Rightarrow\dfrac{OH}{HK}=\dfrac{2}{5}\)
\(S_{AOB}=\dfrac{1}{2}.OH.AB\\ S_{ABCD}=\dfrac{1}{2}\left(AB+CD\right).HK=\dfrac{1}{2}\left(AB+\dfrac{3}{2}AB\right).HK=\dfrac{1}{2}.\dfrac{5}{2}AB.HK\)
\(\Rightarrow\dfrac{S_{AOB}}{S_{ABCD}}=\dfrac{\dfrac{1}{2}OH.AB}{\dfrac{1}{2}HK.\dfrac{5}{2}AB}=\dfrac{2}{5}.\dfrac{1}{\dfrac{5}{2}}=\dfrac{4}{25}\)
\(\Rightarrow S_{ABCD}=\dfrac{4}{\dfrac{4}{25}}=25\)
Bài tập