Cho tam giác ABC nội tiếp (O), AB<AC. Tia phân giác góc A cắt BC tại D, cắt đường tròn tại E. Trên tia AC lấy K: AK=AB.c/m
a) DKCE là tứ giác nội tiếp
b) c/m AK.AC=AD.AE
c)AE2 -BE2= AK.AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 7 2023
a: góc BHD+góc BMD=180 độ
=>BHDM nội tiếp
b: BHDM nội tiếp
=>góc HDM+góc HBM=180 độ
=>góc ADM=góc ABC
=>góc ADM=góc ADC
=>DA là phân giáccủa góc MDC
c: Xét tứ giác DHNC có
góc DHC=góc DNC=90 độ
=>DHNC nội tiếp
=>góc NHD=góc NDC
góc NHD+góc MHD
=180 độ-góc NCD+góc MBD
=180 độ+180 độ-góc ABD-góc ACD
=180 độ
=>M,H,N thẳng hàng
24 tháng 3 2023
Bổ sung: ΔABC cân tại A
ΔABC cân tại A
=>AO đi qua trug diểm I của EF
Vẽ IK vuông góc AB tại K, gọi H và G lần lượt là giao của OA với BC và(O)
Vì OE vuông góc AB, IK vuông goc AB, GB vuông góc AB
=>OE//IK//GB
ΔABG có IK//GB
nên IK/BG=AI/AG
=>IK=AI*BG/AG
ΔABH có EI//BH
ΔABE có OE//BG
=>IH/AH=BE/BA=OG/AG và AE/AB=AI/AH
=>IH=AH*OE/AE
ΔABG có OE//BG
nên AB/AE=BG/OE
AH/AI=AB/AE=BG/OE
=>AH*OE=AI*BG
=>AH*OG=AI*BG
=>IK=IH
=>ĐPCM
CM
17 tháng 5 2019
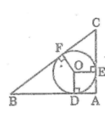
Áp dụng định lí Pitago vào tam giác vuông ABC ta có :
B C 2 = A B 2 + A C 2 = 3 2 + 4 2 = 25
Suy ra : BC = 5 (cm)
Theo tính chất hai tiếp tuyến giao nhau ta có:
AD = AE
BD = BF
CE = CF
Mà: AD = AB – BD
AE = AC – CF
Suy ra: AD + AE = AB – BD + (AC – CF)
= AB + AC – (BD + CF)
= AB + AC – (BF + CF)
= AB + AC – BC
Suy ra:
2 tháng 12 2016
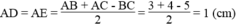
Ta có: AC = 5
Gọi bán kính đường tròn nội tiếp là r
Ta có:
S(ABC) =S(OAB) + S(OAC) +S(OBC) (1)
S(OAB) = r*AB/2
S(OAC) = r*AC/2
S(OBC) = r*BC/2
=> S(OAB) + S(OAC) +S(OBC) = r* (AB+BC+CA)/2 = 6r (2)
Mặt khác; S(ABC) = AB.AC/2 = 6 (3)
Từ (1), (2), (3) :
=> 6r = 6 => r = 1.
Ủng hộ mk nha!
11 tháng 7 2023
a: góc BEH+góc BFH=90 độ
=>BEHF nội tiếp
b: góc ABK=1/2*sđ cung AK=90 độ
Xét ΔABK vuông tại B và ΔAFC vuông tại F có
góc AKB=góc ACF
=>ΔABK đồng dạng với ΔAFC
a: Xét ΔABD và ΔAKD có
AB=AK
\(\widehat{BAD}=\widehat{KAD}\)
AD chung
Do đó: ΔABD=ΔAKD
=>\(\widehat{ABD}=\widehat{AKD}\)
=>\(\widehat{ABC}=\widehat{AKD}\)
mà \(\widehat{AKD}+\widehat{DKC}=180^0\)(hai góc kề bù)
nên \(\widehat{ABC}+\widehat{DKC}=180^0\left(1\right)\)
Xét (O) có
\(\widehat{ABC}\) là góc nội tiếp chắn cung AC
\(\widehat{AEC}\) là góc nội tiếp chắn cung AC
Do đó: \(\widehat{ABC}=\widehat{AEC}=\widehat{DEC}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{DEC}+\widehat{DKC}=180^0\)
=>DKCE là tứ giác nội tiếp
b: Xét ΔAKD và ΔAEC có
\(\widehat{AKD}=\widehat{AEC}\left(=\widehat{ABC}\right)\)
\(\widehat{KAD}\) chung
Do đó: ΔAKD~ΔAEC
=>\(\dfrac{AK}{AE}=\dfrac{AD}{AC}\)
=>\(AK\cdot AC=AD\cdot AE\)