Cho \(\Delta ABC\) đều có cạnh bằng \(2022\) \(cm\) như hình vẽ. Tính diện tích phần tô đen.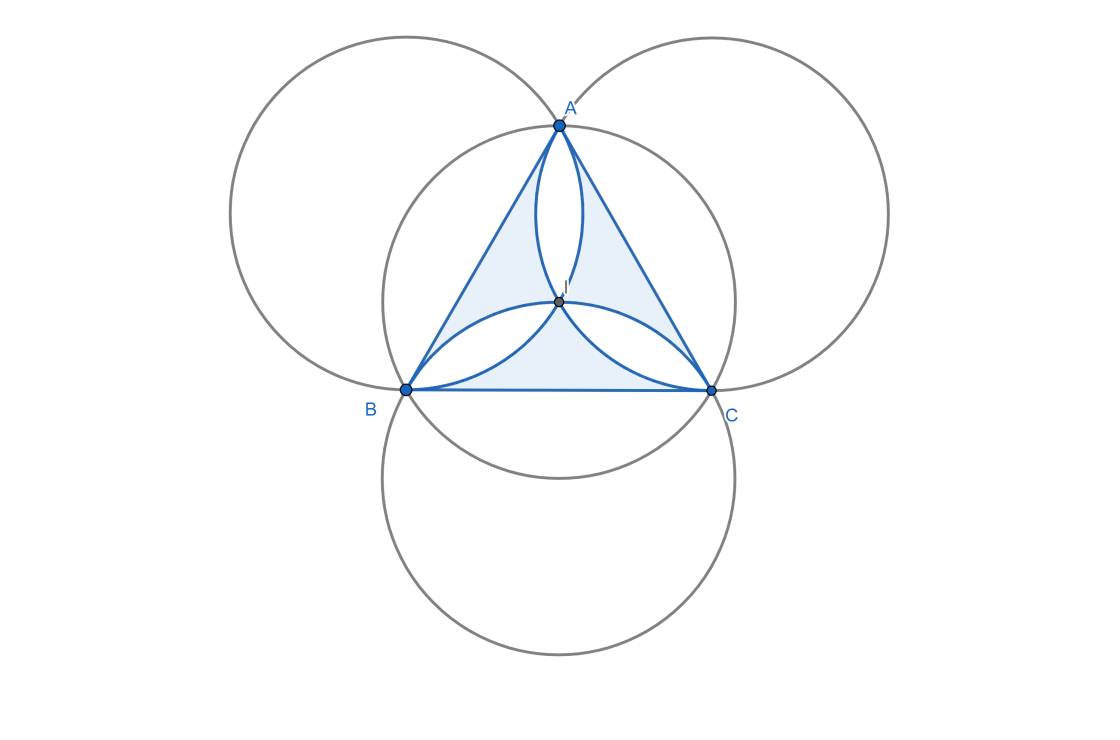
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặng Hồng Thúy sao e kiểu vẻ ta đây vậy,kh giải được thì thôi.

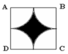
Ta thấy, đường chéo của hình vuông( hình vuông là hình thoi đặc biệt có 2 đường chéo = nhau) bằng đường kính hình vuông
a) Shình vuông là:
6x6=36(cm2)
Vì Shình vuông = Đường chéo T1x Đường chéo T2:2
Mà đường chéo hình vuông= đường kính hình tròn
=> Đường kính hình tròn x Đường kính hình tròn=36x2=72(cm)
Vì đường kính gấp 2 lần bán kính
=> Bán kính x bán kính=72:2:2=18(cm2)
=> Shình tròn =18x3,14=56,52(cm2)
b) Sphần gạch chéo =56,52-36=20,52(cm2)
Đáp số: a) 56,52cm2
b) 20,52 cm2
a: \(AC=\sqrt{6^2+6^2}=6\sqrt{2}\left(cm\right)\)
=>\(OA=3\sqrt{2}\left(cm\right)\)
\(S_O=OA^2\cdot3.14=56.52\left(cm^2\right)\)
b: \(S_{ABCD}=6^2=36\left(cm^2\right)\)
=>Diện tích phần còn lại là \(56.52-36=16.52\left(cm^2\right)\)

a) Diện tích hình tam giác ABC là: 300 (cm 2)
b) Độ dài cạnh CM là: 6 (cm)

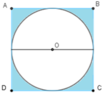
Hình tròn tâm O có đường kính bằng độ dài cạnh hình vuông và bằng 10cm.
Bán kính của hình tròn tâm O là:
10 : 2 = 5 (cm)
Diện tích hình tròn tâm O là:
5 × 5 × 3,14 = 78,5 ( c m 2 )
Diện tích hình vuông ABCD là:
10 × 10 = 100 ( c m 2 )
Diện tích phần tô màu là:
100 − 78,5 = 21,5 ( c m 2 )
Đáp số: 21,5 c m 2

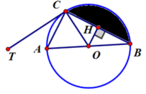
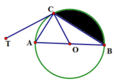
Ta có
T C A ^ = A B C ^ = 30 0 . cos A C B ^ = B C A B = 3 2 ⇒ B C = 3 c m .
Kẻ đường cao OH trong tam giác OBC. Ta có sin O B H ^ = O H O B = 1 2 ⇒ O H = 1 2 c m .
Diện tích tam giác OBC là s 1 = 1 2 . O H . B C = 3 4 c m 2 .
Ta có B O C ^ = 120 0 (vì O B C ^ = B C O ^ = 30 0 ).
Diện tích hình quạt chứa phần tô đen là s 2 = 120 360 . π . R 2 = π 3 c m 2 .
Diện tích phần tô đen là s = s 2 − s 1 = π 3 − 3 4 c m 2 .

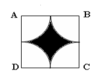
\(S_{ABC}=\dfrac{AB^2\sqrt{3}}{4}\) theo công thức diện tích tam giác đều
Bán kính các hình tròn \(R=\dfrac{2}{3}.\dfrac{AB\sqrt{3}}{2}=\dfrac{AB\sqrt{3}}{3}\)
Do ABC đều \(\Rightarrow sđ\stackrel\frown{AB}=sđ\stackrel\frown{AC}=sđ\stackrel\frown{BC}=\dfrac{360^0}{3}=120^0\)
Gọi O là tâm đường tròn bên trái
\(\Rightarrow sđ\stackrel\frown{AI}=\dfrac{1}{2}sđ\stackrel\frown{AB}=60^0\Rightarrow S_{quạt-OAI}=\dfrac{1}{6}S_{tròn}\) \(=\dfrac{1}{6}.\pi\left(\dfrac{AB\sqrt{3}}{3}\right)^2=\dfrac{\pi.AB^2}{18}\)
\(\Delta OAI\) cân tại O có 1 góc bằng 60 độ nên OAI là tam giác đều
\(\Rightarrow S_{\Delta OAI}=\dfrac{OA^2\sqrt{3}}{4}=\dfrac{R^2\sqrt{3}}{4}=\dfrac{AB^2\sqrt{3}}{12}\)
\(\Rightarrow\) Diện tích phần tô đen:
\(S=S_{ABC}-6\left(S_{quạt-OAI}-S_{\Delta OAI}\right)=\dfrac{AB^2\sqrt{3}}{4}-6\left(\dfrac{\pi AB^2}{18}-\dfrac{AB^2\sqrt{3}}{12}\right)\)
\(=\left(\dfrac{3\sqrt{3}}{4}-\dfrac{\pi}{3}\right)AB^2\)