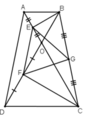
1a/ Cho tam giác đều ABC, trọng tâm G. O là một điểm thuộc miền trong tam giác và O khác G. Đường thẳng OG cắt các đường thẳng BC,BA và AC theo thứ tự ở A',B',C'. Chứng minh rằng \(\frac{OA'}{GA'}+\frac{OB'}{GB'}+\frac{OC'}{GC'}=3\)
b/ Từ một điểm P thuộc miền trong của tam giác đều ABC. Hạ các đường vuông góc PD,PE và PF xuống các cạnh BC,CA và AB. Tính \(\frac{PD+PE+PF}{BD+CE+AF}\)


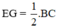 (1)
(1)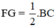 (2)
(2)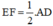
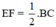 (3)
(3)
a, https://olm.vn/hoi-dap/question/1030999.html
b,\(\frac{\sqrt{3}}{3}\)
CM PD+PE+PF=AH(đường cao)=\(\frac{\sqrt{3}AB}{2}\)
CM BD+CE+AF=\(\frac{3AB}{2}\)
D/s:\(\frac{\sqrt{3}}{3}\)