một vật khối lượng 400 g đang trượt đều trên bề mặt phẳng ngang dưới tác dụng của lực F = 0,4 N. lấy g = 10 m/s^2. Tính hệ số ma sát trượt và mặt phẳng nằm ngang
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/ \(F_k-F_{ms}=m.a\Rightarrow\mu=\dfrac{F_k-m.a}{mg}=...\)
b/ \(F_k.\cos30^0-F_{ms}=m.a\Rightarrow\mu=\dfrac{F_k.\cos30^0-m.a}{mg}\)

Chọn C.
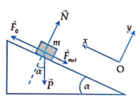
+ Khi vật trượt đều lên mặt phẳng nghiêng:
![]()
Chiếu lên phương mặt phẳng nghiêng và vuông góc với mặt phẳng nghiêng:
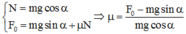
+ Khi vật trượt đều trên mặt ngang:
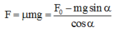

Chọn C.
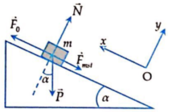
+ Khi vật trượt đều lên mặt phẳng nghiêng:
F 0 ⇀ + P ⇀ + N ⇀ + F m s ⇀ = 0 ⇀
Chiếu lên phương mặt phẳng nghiêng và vuông góc với mặt phẳng nghiêng:
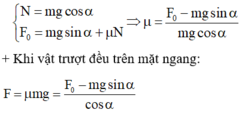

a/ \(F_k-F_{ms}=m.a\Rightarrow a=\dfrac{F_k-\mu mg}{m}=\dfrac{2-0,25.0,5.10}{0,5}=1,5\left(m/s^2\right)\)
b/ \(v=v_0+at=1,5.8=12\left(m/s\right)\)
\(F_{ms}=m.a'\Rightarrow a'=-\dfrac{0,25.0,5.10}{0,5}=-2,5\left(m/s^2\right)\)
\(v''^2-v^2=2aS\Rightarrow S=\dfrac{0-12^2}{2.\left(-2,5\right)}=28,8\left(m\right)\)
\(28,8=vt+\dfrac{1}{2}.a't^2=12.t+\dfrac{1}{2}.\left(-2,5\right).t^2\Rightarrow t=...\left(s\right)\)
\(\Rightarrow S'=v\left(t-1\right)+\dfrac{1}{2}.a'\left(t-1\right)^2=...\left(m\right)\)
\(\Rightarrow\Delta S=S-S'=...\left(m\right)\)

a) Chọn chiều dương là chiều chuyển động của vật (0,25đ)
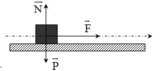
Các lực tác dụng lên vật như hình vẽ :
Theo định luật II Niu tơn: 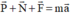 (0,25đ)
(0,25đ)
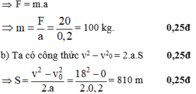
c) Chọn chiều dương là chiều chuyển động của vật
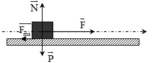
Các lực tác dụng lên vật như hình vẽ: (0,25đ)
Theo định luật II Niu tơn: 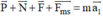 (0,25đ)
(0,25đ)
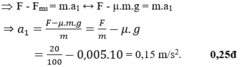

a) Chọn chiều dương là chiều chuyển động của vật (0,25 điểm)
Các lực tác dụng lên vật như hình vẽ:
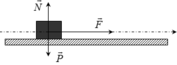
Theo định luật II Niu tơn: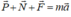 (0,25 điểm)
(0,25 điểm)
⇒ F = m.a
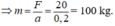
b) ta có công thức v 2 - v 0 2 = 2.a.S (0,25 điểm)
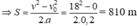
c) Chọn chiều dương là chiều chuyển động của vật
Các lực tác dụng lên vật như hình vẽ: (0,25 điểm)
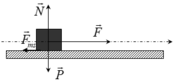
Theo định luật II Niu tơn: 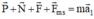 (0,25 điểm)
(0,25 điểm)
⇒ F - Fms = m.a1 ↔ F - μ.m.g = m.a1
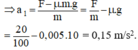 (0,25 điểm)
(0,25 điểm)

Vì vật trượt trên mặt phẳng nằm ngang \(\Rightarrow g=a=10\left(m/s^2\right)\)
Ta có : \(\overrightarrow{P}+\overrightarrow{N}+\overrightarrow{F_{ms}}+\overrightarrow{F_k}=m\overrightarrow{a}\)
Chiếu \(\left\{{}\begin{matrix}Ox:F_k-F_{ms}=ma\left(1\right)\\Oy:-P+N=0\left(2\right)\end{matrix}\right.\)
Từ (1) \(\Rightarrow0,4-F_{ms}=0,4.10\\ \Rightarrow F_{ms}=3,6\left(N\right)\)
(2) \(\Rightarrow P=N=m.g\Rightarrow F_{ms}=\mu.m.g\Rightarrow\mu=0,9\)